Sécurité Passive / Approche Locale
Méthode des éléments finis à schéma implicite
Ces méthodes utilisent :
Une discrétisation spatiale par éléments finis,
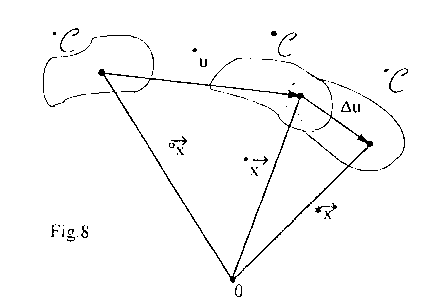
Une discrétisation temporelle à schéma implicite, correspondant donc à une résolution itérative d'une équation implicite écrite à partir des équilibres aux temps t' et t*=t'+dt, par convergence des déplacements *Δun -> *Δun+1, à chaque pas de temps permettant ainsi de connaître les contraintes à chaque pas de temps
Et donc trois boucles de résolution dans les logiciels correspondants:
-Une boucle externe de réactualisation de la géométrie, avec les chargements associés
-Une boucle interne de réactualisation des propriétés du matériau
-La boucle itérative implicite t' -> t*
-Parfois une boucle supplémentaire pour réactualiser les conditions aux limites
Ces méthodes à schéma implicite sont inconditionnellement stables dans le temps et peuvent donc être utilisées avec un pas de temps quelconque en théorie. Elles sont donc réservées aux études de chocs relativement lents, dune durée supérieure à la seconde.
Application de ce schéma d'intégration implicite sur un exemple du type masse-ressort
Soit la même équation différentielle que précédemment,
![]()
et soit l'axe de temps discrétisé suivant :
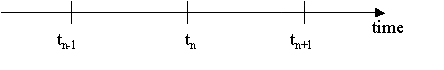
On connaît |
| et l'on recherche | et |
L'équilibre dynamique à l'instant |
s'écrit : |
![]()
Où |
est inconnu. Une résolution directe pour |
et |
est alors impossible. |
A présent on peut appliquer la méthode des différences avant :
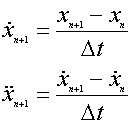
d'où
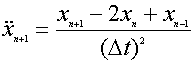
Qui donne après substitution
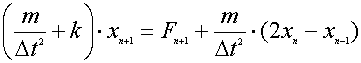
on peut résoudre cette équation pour un déplacement à l'instant |
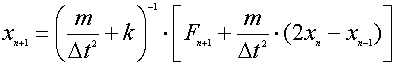
Pour un système à plusieurs degrés de liberté,
cette opération donne la solution d'un système à équations
algébriques.
On peut alors obtenir les autres variables, en posant :
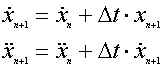
Ce schéma ne dépend pas du pas de temps Δt
ce schéma implicite est dit inconditionnellement stable.