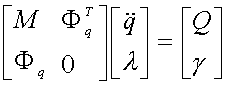Dynamique plane d'un système multicorps rigides articulés
Équations de contraintes dans un plan
Les coordonnées utilisées pour définir la position absolue et la rotation de chaque corps rigide se notent pour le corps i sous forme d'un vecteur qi :
![]()
Le système contient Nc corps rigides. Le vecteur de coordonnées généralisées de dimension 3Nc=N s'écrit:
![]()
Lorsque deux corps rigides sont en contact, ils se forment un joint ou liaison cinématique. Un assemblage de corps rigides interconnectés par des joints s'appelle une chaîne cinématique. Le système mécanique est formé quand au moins un des corps rigides de la chaîne cinématique est fixé et quant au moins un des corps rigides peut se mouvoir. Le nombre minimum de coordonnées généralisées nécessaire pour décrire la configuration du système correspond au nombre de degrés de liberté. Pour que les joints imposent un comportement particulier aux corps rigides qu'ils connectent, des contraintes sont imposées sur ces corps rigides et diminuent leur nombre de degrés de liberté. Lorsque ces conditions sont exprimés de façon analytique, ce sont des équations de contraintes. Une équation de contrainte impose une condition sur le vecteur q des coordonnées généralisées du système et s'écrit :
![]()
Cette contrainte est dite scléronome car elle est stationnaire. lorsque la variable temps intervient, elle est rhéonome et s'écrit :
![]()
Si la contrainte est doublement continûment différentiable, elle est holonome. Si l'équation de contrainte contient des relations en vitesse, c'est une contrainte non holonome et se note :
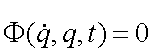
Dans notre cas, nous utilisons des contraintes holonomes de type rhéonomes et nous notons le vecteur équations de contrainte :
![]()
Nh est le nombre d'équations de contraintes. Ainsi, le nombre de degré de liberté Nddl du système est égal à Nddl=N-Nh
Si Nddl est strictement positif, le système est un mécanisme.
Si Nddl est nul, le système est isostatique.
Si Nddl est strictement négatif, le système est hyperstatique.
Si l'on dérive par rapport au temps |
|
, nous obtenons l'équation en vitesse : |
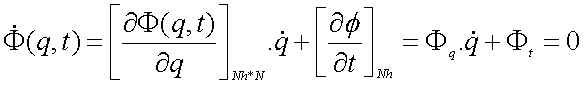
La dérivation par rapport au temps de l'équation en vitesse donne l'équation en accélération :
![]()
Pour simplifier, nous introduisons le vecteur |
|
: |
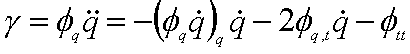
Équation du mouvement dans le plan d'un système multicorps rigides articulés
Le travail virtuel |
|
des forces Fi et moments externes ni agissant sur le corps rigide i peut s'écrire en termes de |
|||
déplacements cartésiens virtuels |
|
et de rotation virtuelle |
|
compatibles avec les contraintes. |
|
Pour un système composé de NC corps rigides, la somme des travaux virtuels s'écrit :
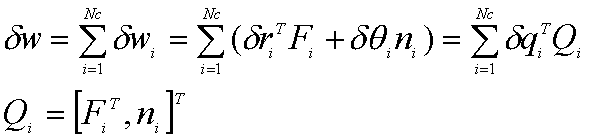
Si nous notons :
![]()
les équations virtuelles peuvent s'écrire pour tout déplacement virtuel |
|
compatible avec les contraintes : |
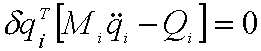
Pour i=1, ..., NC
Nous considérons maintenant l'effet des efforts de réaction dans les liaisons cinématiques.
Les contraintes |
|
étant parfaites (sans jeu et sans frottement), |
la somme des travaux virtuels effectués par les réactions des contraintes le long de n'importe quels déplacements virtuels compatibles avec ces contraintes est nulle en vertu de la troisième loi de Newton (principe de l'action et de la réaction). Cela s'écrit :
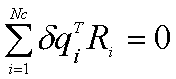
Les équations virtuelles peuvent donc se réécrire pour tout déplacement virtuel |
|
compatible avec les contraintes : |
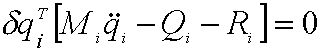
Pour i=1, ..., NC
nous retrouvons ici le principe de d'Alembert dans le cas d'un système muni de contraintes parfaites.
Afin de déterminer les efforts de contraintes, nous allons introduire NH fonctions auxiliaires appelées multiplicateurs de Lagrange qui relient les contraintes sous forme différentielle aux efforts de contraintes à déterminer.
Un déplacement virtuel |
|
compatible avec les contraintes vérifie la relation : |
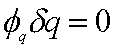
Cette relation correspond aux équations de contraintes exprimées sous forme différentielle. Le système s'écrit donc comme suit :
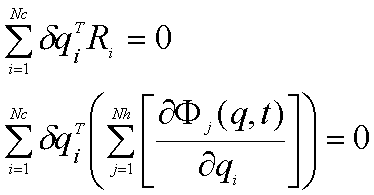
Après introduction des multiplicateurs de Lagrange nous obtenons :
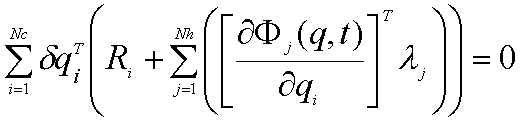 |
où |
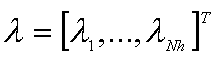 |

Pour i=1, ..., NC
Si nous notons :
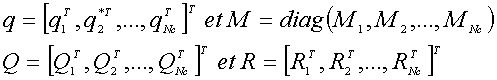
Les équations variationnelles se mettent sous la forme suivante pour tout déplacement virtuel compatible avec les contraintes : |
|
![]()
|
étant arbitraire, le coefficient de |
|
doit être nul, ce qui donne : |
![]()
Ce système de N équations est composés de N+NH inconnues. Ainsi, nous complétons les NH équations manquantes par les NH |
||
équations en accélérations |
|
Le système complet s'exprime donc de la façon suivante : |