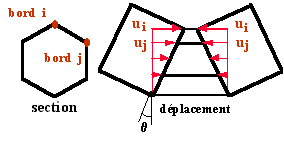
Modèle Analytique en Flexion pure

 

Historique de déformation en trois phases

 

 

 

 

 

	Sommaire
	Phase de pré-effondrement et Phase d'effondrement
	Phase de post-effondrement

 

 

 

 

 

 

 

 

 

 

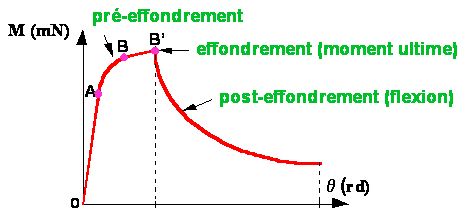
1 - Phase de pré-effondrement et Phase d'effondrement (sommaire)

 

Hypothèses:

- BERNOUILLI : cisaillement nul
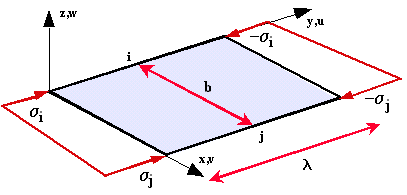
- Section considérée comme un assemblage de plaques avec conditions aux limites
- Chaque plaque est soumise à un chargement qui dépend de sa position par rapport à la fibre   neutre

 

Champ de répartition des contraintes dans une plaque située à une distance y de la fibre neutre

 

Énergie potentielle totale

 

L’état d’équilibre minimise la fonctionnelle

l’équation d’équilibre s’écrit: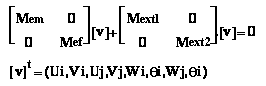

 

Assemblage des matrices pour toutes les plaques

Après assemblage, cette équation peut s’exprimer en fonction de la contrainte critique

 

 

Résolution par itération inverse du système aux valeurs propres

minimise la longueur d’onde de flambement

Vecteur propre -> Mode de Voilement

 

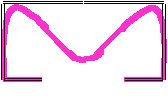
Contrainte située dans le domaine élastique ou plastique
On a donc un flambement élastique ou plastique

 

 

 

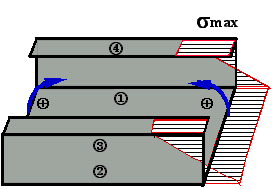
2 - Phase de post-effondrement (sommaire)

 

Étude du faciès de déformation ( Modèles cinématiques en flexion )

(Kecman 1979)+ limité aux sections rectangulaires
(Anceau 1994)+ limités aux sections U, H et W

 

 

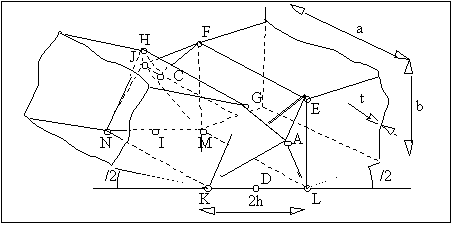Développement d’un modèle généralisé pour des sections arbitraires

 

Étude de la flexion d’une section quelconque

 

En fonction de leur position par rapport à la fibre neutre, les plaques du profilé subissent des chargements de compression (ui différent de 0) et de flexion (ui différent uj )

 

La superposition du modèle cinématique en flexion de Kecman et du modèle quasi-inextensible de Wierzbicki et Abramowicz aboutit à 5 mécanismes de base.

 

 

 

La section ne peut être décomposée en éléments coins (coupure lignes de pliage du modèle Kecman).

Décomposition en éléments plaques avec Conditions aux Limites.

Le mode de voilement permet de choisir le mécanisme d’effondrement de chaque plaque.

Formulation des zones de dissipation énergétique.

Théorème des puissances virtuelles, d'où le calcul de la réponse instantanée en moment M(teta).

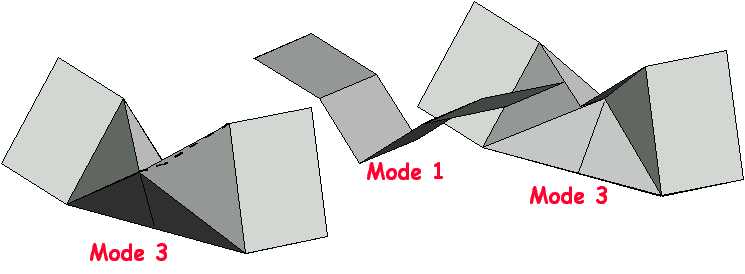
Décomposition du mode de voilement en modèles cinématiques.

 

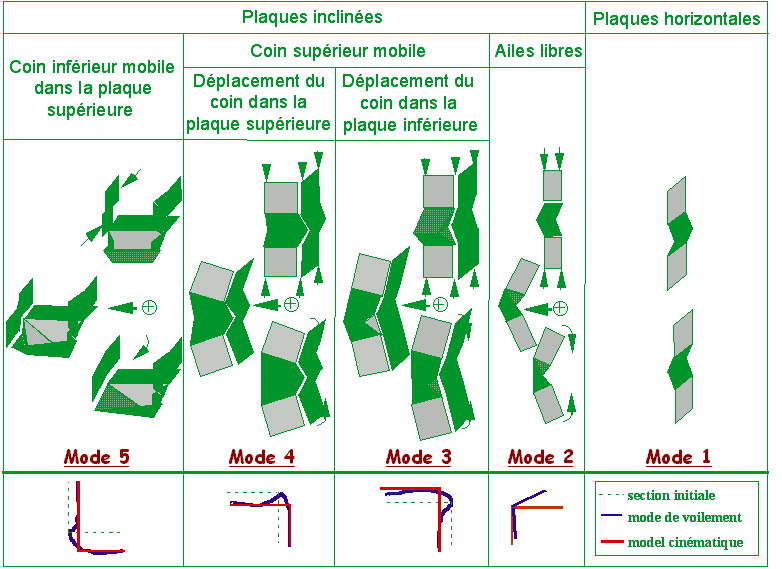
Illustration du choix des modèles cinématiques de plaques

Comportement déterminé pour chaque coin en comparant les déplacements transversaux des plaques

 

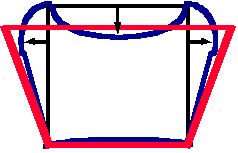
Recherche parmi les 5 mécanismes de base, du mode cinématique correspondant à chaque plaque

 

.