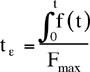Critères de blessure

 

 

	Sommaire
	Tête
	Cou
	Thorax et Bassin
	Ensemble genou-fémur-tibia

 

 

Généralités

Un critère est ce qui permet de porter un jugement d'appréciation.

Pour mesurer les modifications apportées à un environnement homme-siège, il est nécessaire d'utiliser les critères biomécaniques. Ces indices prédictifs de blessure sont bâtis par comparaison des variables qui caractérisent la réponse mécanique du corps humain avec la gravité des lésions produites.
La figure suivante représente la forme que peut prendre un critère biomécanique :

 

 

 L'échelle des abscisses représente la valeur du critère, et l'échelle des ordonnées, un niveau de blessure sur l'échelle AIS. Un bon critère est celui qui prédit un niveau de blessure de plus en plus élevé (AIS augmente) au fur et à mesure que sa valeur augmente (critère augmente). La valeur généralement choisie pour séparer les blessures de faible sévérité des autres est l'AIS=3.

 Un critère biomécanique général indiquant l'état d'un passager après un choc n'existe pas, et ne peut pas exister. En effet, étant donné la diversité des tissus qui composent le corps humain, et les multiples cas de chargement qui peuvent se présenter, il est nécessaire d'étudier chaque cas séparément.

 Ceci nous oblige donc à classer les critères suivant le segment corporel auquel ils s'appliquent. Mais cela ne suffit pas encore car pour un même segment, plusieurs types de mécanismes peuvent produire des blessures différentes. La variable qui rend le mieux compte de la violence des phénomènes et de la probabilité de lésion n'est pas toujours la même.

Il est donc nécessaire de travailler segment par segment pour estimer un risque de blessure, et pour chacun de prendre en compte les différents types de blessure et les différents mécanismes de production. Les critères de tests s'intéressent plus particulièrement à différentes parties du corps humain : la tête, le cou, le thorax et les ensembles bassin-hanche, genou-fémur-tibia et cheville-pied.

 

 

 

 

La tête (sommaire)

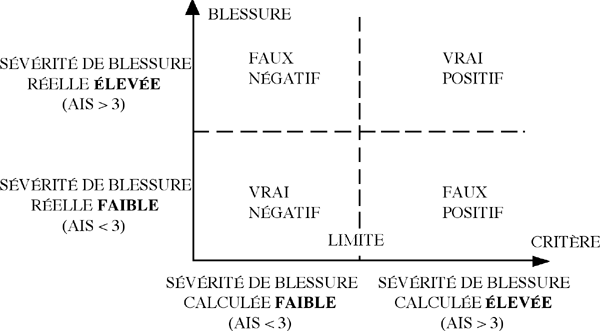
De nombreux critères ont été développés pour rendre compte de la probabilité de blessure de la tête. La plupart d'entre eux ont été dérivés d'une courbe de tolérance établie dans les années 60 aux Etats-Unis et appelée la courbe de Wayne State (WSTC). Cette courbe représente l'accélération effective (en g) en fonction du temps pour établir un niveau de tolérance à la fracture du crâne. Cette courbe a été établie en faisant des liens entre fractures sur cadavres et fractures sur humains vivants.

 

 

 Provenant de données expérimentales, cette courbe ne considère pas le ou les mécanismes en cause. Nous pouvons reprocher la non-homogénéité des données expérimentales. Elles proviennent d'impact de la tête contre une surface infiniment rigide, sur le cadavre ou sur l'animal, pour les plus fortes accélérations et d'essais sur des volontaires pour les plus faibles, mais sans impact. La courbe traduit la survenue ou non d'une commotion. Les deux critères les plus connus basés sur la WSTC sont, le Gadd Severity Index (GSI), qui est une approximation grossière de la WSTC, et le Head Injury Criterion (HIC), actuellement le critère le plus utilisé.

 

Accélération linéaire : du SI au HIC.

Gadd souligne que ni l'accélération moyenne, ni le pic d'accélération observé pendant la phase d'impact ne suffisent pour décrire correctement la réponse de la tête en terme de blessure. Il explique que la probable blessure résultante dépend fortement de la forme du signal de l'accélération et affirme que pour des accélérations moyennes identiques issues de signaux différents, les effets ne sont pas comparables. Pour tenir compte de la forme du signal de l'accélération et de la durée d'application, Gadd propose d'intégrer l'accélération sur la durée entière du signal. Comme le risque lésionnel est, selon lui, une fonction non linéaire de l'accélération, il suggère d'appliquer un facteur de puissance sur l'accélération (supérieur à 1) et d'intégrer le résultat sur la durée totale du signal.

Cette étude conduit au seuil de blessure suivant :

 

Où : a : accélération (g),        n : facteur de puissance supérieur à 1,        t : temps (s)

 

 

 

 La représentation de cette expression sur un graphe à double échelle logarithmique est une droite à condition de choisir le facteur n comme constant. Gadd représente sur le même type de graphique la courbe de la " Wayne state University " et montre que la pente de la droite obtenue est de l'ordre de 2.5. Il formule le critère de blessure suivant connu sous le nom de Gadd Severity Index :

 

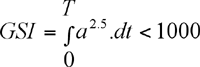avec T :durée de l'impulsion (s)

 

 

 Gadd considère que l'approximation de la courbe de la " Wayne State University " comme une ligne droite est acceptable à l'époque où il effectue ses travaux et en profite pour rappeler la disparité des données qui ont permis d'élaborer cette courbe.
Pour définir la tolérance à 1000, il s'appuie sur les travaux réalisés par Eiband en 1959 et Swearingen en 1965. En 1971, Gadd ajuste le seuil de tolérance et le définit maintenant à 1500 pour des sollicitations sans contact de la tête. La même année, Versace suggère le critère de blessure suivant :

 

Basé sur les critiques de Versacesur le (G)SI, au NHTSA, on suggère en 1972 que le " Severity Index " soit remplacé par un critère de blessures modifié, connu aujourd'hui sous le nom de " Head Injury Criterion " :

 

 

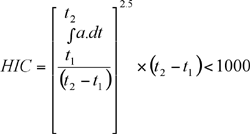
avec t1 et t2 qui définissent le temps de début et de fin de contact de la tête : t2 - t1 < 36 ms,
a : accélération linéaire résultante exprimée au centre de gravité de la tête en g.

 

 

Dans le cas des tests effectués avec des mannequins, c'est le HIC(d) (dummy) qui est calculé et sa valeur ne doit pas dépasser 1000.

 

HIC(d) = 0.75446 (HIC) + 166.4 < 1000

 

Une valeur de HIC est juste une indication mais elle ne correspond pas à une blessure : il ne s'agit pas d'une échelle de blessure mais d'une échelle de gravité.

En effet, le calcul du HIC dans de nombreux essais biomécaniques et dans des simulations d'essais " chariot " a montré que ce critère ne présentait aucune corrélation avec la gravité des blessures. Nous pouvons d'ailleurs remarquer l'absence de corrélation entre les valeurs du HIC et l'échelle AIS. Nous notons dans les exemples cités par Ballas et Ramet ceci : nous pouvons obtenir un AIS 0 pour des valeurs de HIC variant de 67 à 4787. Mais inversement à partir de reconstructions d'accidents avec mannequins et cadavres, Césari trouve un HIC 500 provoquant des blessures graves.
Malgré la définition du critère, qui indique si l'on est au dessus ou en dessous d'un seuil, certains proposent une utilisation du HIC en continu. La figure suivante montre un risque de blessure en fonction d'une valeur du HIC.

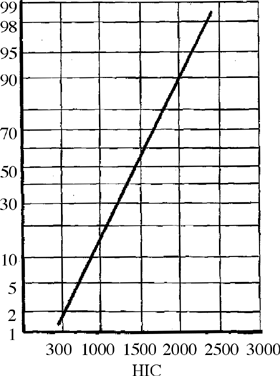
Exemple d'utilisation linéaire du HIC

 Bien entendu, un bon nombre de facteurs peuvent influencer la valeur du HIC, comme l'âge du fait de la diminution des caractéristiques osseuses, ou encore les forces de retenue ou de chargement de la tête par le cou.

 

 

Accélération angulaire : le GAMBIT.

Les critères associés aux modèles unidirectionnels ne prennent pas en compte l'accélération angulaire. L'accélération linéaire peut être remise en cause, car elle est ramenée au centre de gravité de la tête, alors que les directions d'impact sont en général non centrées et entraînent une rotation de la tête, donc une accélération angulaire. Celle-ci est considérée comme étant un facteur non négligeable pour l'apparition des blessures vasculaires et neurologiques.

Ommaya en 1984 propose de prendre une limite de tolérance pour une accélération angulaire pure et pour une accélération linéaire pure, mais sans préciser laquelle. Lowenhielm en 1975 propose lui un pic d'accélération angulaire à 4500 rad/s2 entraînant une vitesse de 70 rad/s minimum pour avoir contusion.

Il existe un critère qui prend en compte les accélérations linéaires et angulaires, le " Generalized Acceleration Model for Brain Injury Threshold " (GAMBIT). Le GAMBIT suppose en particulier que les blessures au cerveau apparaissent lorsque les effets combinés des accélérations linéaires et angulaires dépassent une valeur limite g1 ou g2.

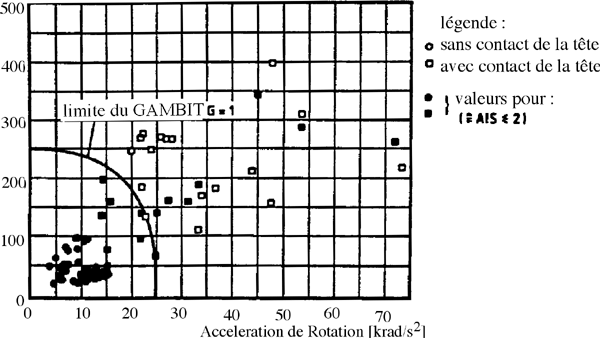
La limite g1 correspond à une pondération égale pour l'accélération linéaire et l'accélération angulaire. Dans un plan accélération linéaire/angulaire, une droite est tracée, allant d'une valeur limite proposée en accélération purement linéaire à une valeur limite en accélération purement angulaire. La limite g2 correspond à une ellipse dans ce même plan.

 

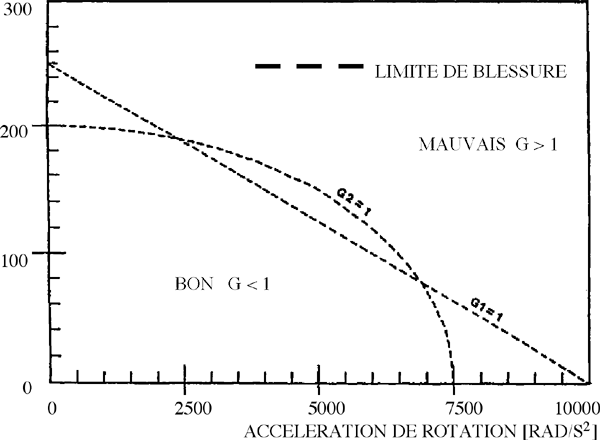
Limites pour le GAMBIT. g1 : linéaire, g2 : elliptique

 

D'après l'auteur, les limites de son modèle sont les limites de notre connaissance dans la tolérance de la tête à un impact, et en particulier dans les zones grande translation/faible rotation et faible translation/grande rotation.

 

La définition d'une ligne droite comme zone de tolérance se définit :

- Acc. Linéaire : limite de 250 g qui est logique avec le critère de rupture employé dans l'estimation des casques où le mouvement est purement linéaire,

- Acc. Angulaire : 10000 rad/s2 qui est dans la gamme des valeurs généralement admises.

Le critère devient :

 

Nous notons que le GAMBIT ne tient pas compte de la durée d'application de l'accélération. D'après Newman, les études expérimentales montrent qu'il suffit de prendre la valeur maximum de la courbe accélération angulaire/accélération linéaire, et de vérifier de quel côté elle se trouve par rapport à la frontière.

 

La définition du GAMBIT a été revue en 1990 par Kramer et Appel.

 

 

 D'après une étude statistique d'accidents reconstitués numériquement, ils sont remontés à l'accélération subie par la tête de l'occupant. Connaissant les blessures réelles des accidentés de la route, ils ont lancé un calcul d'optimisation qui a redéfini le GAMBIT sur des bases expérimentales. Il est maintenant défini par :

 

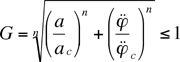avec n=2,5, ac=250g, =25krad/s2

 

 

 

 

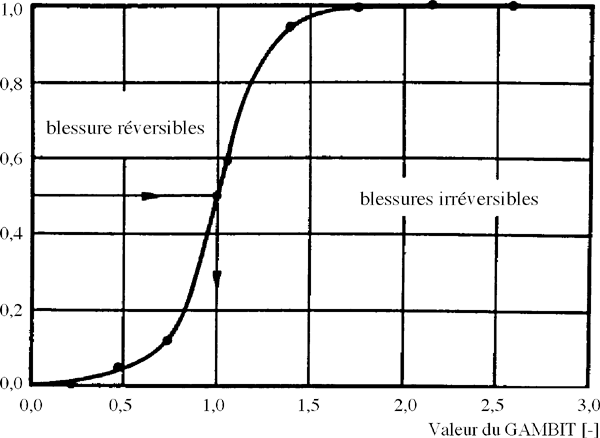
Probabilité de blessure en fonction de la valeur du GAMBIT. La valeur seuil du critère est 1

 

 

 

Le cou (sommaire)

 

Cinématique du coup du lapin

Nygren et al. ont montré que les blessures au cou jusqu'alors peu prises en considération par le corps médical et codées AIS 1 conduisent souvent à des dysfonctionnements permanents. En effet, ces blessures supposées être des dommages aux ligaments et aux muscles ne laissent aucune indication ni visible sur les radiographies, ni palpables. Le codage n'est pas approprié car des douleurs peuvent être ressenties encore des mois après l'accident.

Sur un échantillon de 340.000 accidents, les auteurs constatent qu'une blessure légère au cou survient en collision frontale pour un occupant ceinturé alors que les plus sévères surviennent en collision par l'arrière pour un occupant non ceinturé.

La cinématique du "coup du lapin" peut se décomposer comme suit, pour un passager assis dans une voiture qui se fait tamponner par l'arrière :
     · Le "crash" contraint le tronc à accélérer vers l'avant, poussé par le dossier du siège, ce qui entraîne un cisaillement du cou,
     · La tête ne peut pas suivre ce mouvement, ce qui provoque une hyper extension du cou (vers l'arrière), relativement au tronc,
     · Le tronc est ensuite retenu par la ceinture, la tête bouge alors rapidement vers l'avant, ce qui implique une hyper flexion.

L'étude de Nygren montre que la variation de l'incidence des blessures au cou dans les collisions arrières est influencée par de nombreux facteurs : poids du véhicule, distance horizontale et verticale entre la tête et le repose tête.

 

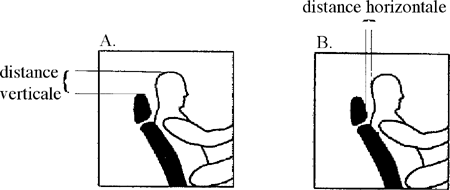
Position verticale (a) et horizontale (b) entre la tête et le repose-tête

Le repose-tête a une influence certaine sur l'apparition des blessures, en particulier la distance verticale, car il limite le mouvement de la tête vers l'arrière. Nygren conclut qu'un repose-tête fixe est plus utile qu'un repose-tête réglable qui n'est, dans la pratique, jamais réglé correctement.

Un étude récente montre que la distance horizontale est aussi un facteur important. Il existe une corrélation entre les victimes qui ont des douleurs pendant plus d'un an, et celles qui avaient au moment de l'accident une distance horizontale supérieure à 10 centimètres.

 

 

Tolérance du cou

Il existe dans la littérature de nombreuses données sur la tolérance du cou, mais elles concernent essentiellement des volontaires. Si ces données sont intéressantes pour comprendre la cinématique du cou soumis à des chargements inertiels, elles ne permettent pas d'extrapoler aux zones dangereuses, à cause de la non linéarité du système.

Le type de blessure le plus sérieux du cou est la fracture des vertèbres, qui est le plus souvent due à une contusion, un écrasement, ou un cisaillement, et qui peut toucher la moelle épinière.

Les études montrent que l'angle relatif entre le tronc et la tête peut dépasser 120° lors du coup du lapin. Ce mouvement peut heureusement être limité par des systèmes adaptés. Une mesure plus sûre de la tolérance du cou que l'angle relatif, est la valeur du moment au niveau du condyle occipital (base de la tête).

L'influence des muscles du cou sur sa rigidification est faible, à cause de leur lenteur de mise en route par rapport à une durée de crash.
Voici un corridor (moment = f(angle)), proposé en flexion et extension du cou.

 

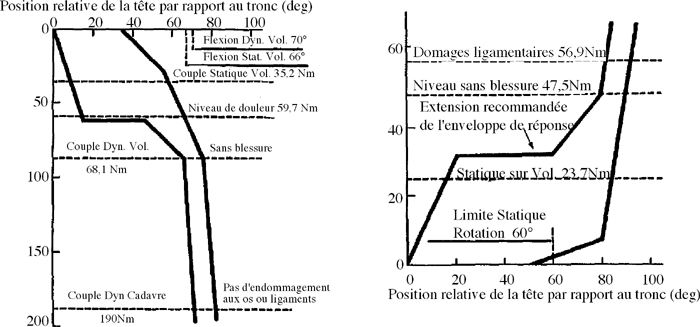
Corridor de protection du cou en flexion et extension

 

Mertz propose une valeur limite du moment mesuré en haut du cou, à ne pas dépasser, en flexion et en extension :
           · Moment de flexion du cou : 190 Nm,
           · Moment d'extension du cou : 57 Nm.

Ces valeurs ont été proposées pour la norme ISO : ISO/TC22/SC12/WG5/N312. Notons que ces valeurs correspondent aux valeurs maximum du corridor présenté ci-dessus.

S'il s'agit d'un impact, représentant une charge répartie, sur la face avant du cou, une valeur de 400N correspond à l'initialisation de fracture des ligaments, et reste en dessous d'un seuil d'écrasement trop important du larynx.

 

 

 

 

Le thorax et le bassin (sommaire)

A la suite des progrès réalisés dans la protection au choc frontal, les biomécaniciens se sont intéressés aux problèmes posés par le choc latéral. Une étude des conditions et des mécanismes de blessures a montré que la gravité d'un choc latéral était directement liée à la vitesse de déplacement de la paroi au moment où elle vient heurter l'occupant assis derrière celle-ci. Cet occupant subit des blessures localisées en priorité sur son côté proche de la paroi, au niveau de la tête, du thorax, de l'abdomen et du bassin. En complément de la diminution de la vitesse de la paroi, il est nécessaire d'amortir le choc entre la paroi et l'occupant. On a donc besoin de connaître la tolérance humaine pour pouvoir choisir les caractéristiques du matériau amortissant à utiliser.

Des tests sur être humain montrent qu'une compression de 20% du thorax est sans risque et entièrement réversible. Sur cadavre, avec les limitations dues à ce type d'essai, à 40% de compression, il y a de nombreuses fractures, et la cage thoracique n'assure plus sa fonction protectrice.

Un taux de compression de 35 % est alors proposé comme niveau de tolérance approprié pour la poitrine. Cependant, se pose le problème de la mesure correcte de l'enfoncement.

 Il a été montré que pour un taux de déformation <3m/s, la tolérance de la cage thoracique peut être estimée par sa compression maximum. Cependant, à cause de la viscosité du thorax, le taux de déformation a une grande importance sur la tolérance à la compression, et donc sur les risques de blessure des tissus mous.

Pour les impacts ayant un taux de déformation supérieur à 4m/s, un critère doit prendre en compte la déformation et le taux de déformation. Viano et Lau ont ainsi mis au point le Viscous Criterion, basé sur l'énergie dissipée par le thorax.

La définition de la réponse visqueuse est définie par :

 

D : épaisseur extérieure initiale de l'objet Y : déformation instantanée de l'objet

 

 

En utilisant le concept d'énergie stockée (ressort) et d'énergie dissipée (amortisseur), quatre critères sont écrits.

Les coefficients a1 à a4 sont des coefficients de proportionnalité.

 

 

-Critère d'énergie stockée : SEC :

 Limité par l'enfoncement maximum du thorax, il est identique au critère de compression maximum.

 

-Critère du taux de stockage de l'énergie : ESRC :

 En normant par rapport à l'épaisseur extérieure, nous retrouvons le viscous criterion. Ce critère prédit une blessure à l'écrasement, fonction du taux d'écrasement. La limite proposée par Viano est : VCmax=1m/s pour 50% de risque de blessure sévère.

- Critère d'énergie dissipée : DEC :

Limité par le taux maximum de déformation, c'est le critère de vitesse maximum, ou critère de puissance.

 

- Critère de taux de dissipation de l'énergie : EDRC :

Il donne un seuil pour les blessures en cas de choc très violent.

 

Impacteurs		(vc)max.
20 kg, 7m/s	1.00	1.00	1.00	1.00
8kg, 11m/s	1.05	1.63	1.54	2.23
4,35kg, 15m/s	0.96	2.24	1.93	3.61

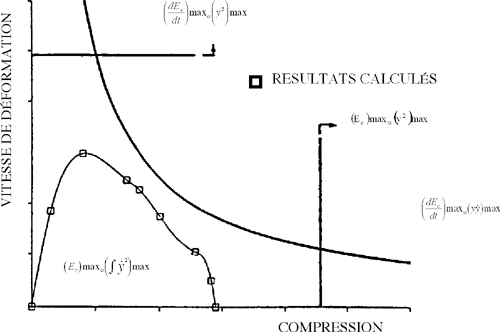
Niveaux de blessure pour les corps déformable

 

Ces quatre critères forment une base solide pour prédire les risques.

Si la courbe "compression - vitesse de déformation" du thorax est dans la région définie par les axes compression, vitesse et les seuils SEC, ESRC et EDRC et que la surface sous la courbe est inférieure au seuil du DEC, alors le risque est faible.

Pour prédire la probabilité de blessures sérieuses sur les os du thorax suite à un impact latéral, une nouvelle mesure appelée Thoracic Trauma Index (TTI) a été proposée en 1984 par Eppinger et al.

Le TTI est un critère basé sur l'accélération de la plus basse vertèbre et celle des cotes. Il tient compte également du poids et de l'âge de la victime d'accident. Ce critère a été élaboré suite à une série de tests biomécaniques effectués sur 84 cadavres. Ces tests ont montrés que l'apparition de blessures au niveau de la cage thoracique est fortement liée au pic d'accélération latérale subi lors de l'impact.

 

Le TTI défini par Morgan s'écrit :

 

TTI = 1.4 (AGE) + 0.5 (RIBg + T12g).(MASS/MSTD)

Où :
AGE : est l'âge de la victime en années,
RIBg : est la valeur maximale de l'accélération en g dans la direction latérale de la 4ème et de la 8ème cote du côté impacté,
T12g : est la valeur maximale de l'accélération en g dans la direction latérale de la 12ème vertèbre,
MASS : est la masse de la victime en kg,
MSTD : est la masse de référence de 75 kg.

Il existe, comme pour le HIC, une définition du TTI pour les mannequins, qui n'ont pas d'âge significatif et dont la masse correspond à la masse de référence (75 kg). Ce critère, le TTI(d) est donc défini pour un mannequin de type 50th percentile par la formule suivante :

TTI(d) = 0.5 * (RIBg + T12g) < 85 à 90 g

Pour respecter la norme FMVSS 214 de 1990, la valeur du TTI(d) ne doit pas dépasser la valeur limite de 85g pour les véhicules 4 portes et celle de 90g pour les véhicules 2 portes.

 

Un autre critère de blessure basé sur l'accélération latérale a été développé par Cavanaugh et al. en 1993.

Ce critère appelé Average Spine Acceleration (ASA) est obtenu de la manière suivante :

 

- Filtrage de l'accélération latérale de la 12ème vertèbre à 300 Hz, - Intégration de l'accélération filtrée pour obtenir la vitesse de la vertèbre, - Calcul de la pente de la vitesse de la vertèbre entre deux points spécifiques.

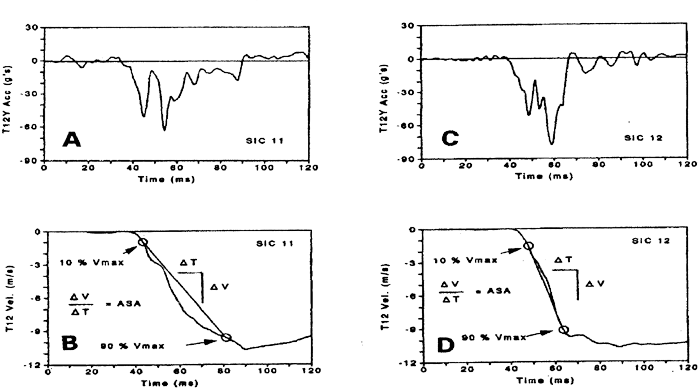
Exemples de calculs de l'ASA pour deux paddings de nature différentes

 

La pente calculée représente donc l'ASA. ASA10 est calculée entre 10 et 90% du pic de vitesse de la vertèbre, ASA15 entre 15 et 85% du pic de vitesse de la vertèbre et ASA20 entre 20 et 80% du pic de vitesse de la vertèbre.

 

L'ASA peut, comme le TTI, tenir compte de l'âge et de la masse de la victime d'accident ; sa formule sera alors la suivante :

 

ASAA,M = ASA * (AGE/45) * (MASS/MSTD)

 

Dans la plupart des cas, le torse peut supporter un niveau d'accélération de 60 à 80g si l'effort est réparti. Cependant, une valeur de ASAA,M inférieure à 30g est bien tolérée par le cadavre humain alors qu'une valeur comprise entre 30 et 40g représente déjà une zone de transition. Au-delà de 40g, des blessures de niveau 4 et 5 sur l'échelle AIS apparaissent. La valeur limite de 30g pour ce critère a donc été proposée dans le cas de choc latéral.

 

En ce qui concerne la tolérance des organes abdominaux, elle est difficile à estimer car ceux-ci sont très mobiles. En effet, lorsqu'il y a compression de l'abdomen, un organe peut bouger et éviter d'être comprimé par l'impacteur, mais ses attaches peuvent alors se rompre.

 

Malgré les difficultés, des chercheurs tentent de déterminer des valeurs limites en compression et en niveau d'effort. Des constructeurs s'intéressent fortement à cette partie du corps humain, notamment en cas de choc latéral.

Sur la base de 6 sujets testés en choc latéral, il a été possible d'établir des relations entre les différents paramètres mécaniques. La conclusion de leur étude concerne les trois critères suivants :

- Un niveau d'effort maximum de 440 daN correspondant à une blessure de type AIS3 a été corrélé avec les résultats donnés par Walfish, - Une valeur limite de déflection de 60 mm a également été vérifiée, - La valeur du critère visqueux VC trouvée est la même que celle donnée par Viano ; cette valeur limite étant fixée à VC =   1.98 m/s

 

 

 

 

 

L'ensemble genou-fémur-tibia (sommaire)

L'ensemble genou-fémur-tibia constitue la troisième partie du corps susceptible d'être touchée lors d'une collision
Viano en 1977 propose un premier critère : le Femur Injury Criterion (FIC) :

 

t<20ms : f=a-b*t	avec a=23.1 kN, et b=0,71 kN/ms
t=20ms : f=8.9 kN

 

L'étude de Leung et al. porte sur la reconstitution de tests sur des mannequins et cadavres. La tolérance à la fracture dépend en grande partie des conditions des os du sujet. Pour prédire le risque de fracture pour toute une population, une étude de minéralisation et de robustesse des fémurs a été menée parallèlement aux essais.

Un critère a été mis au point : le Knee-Thigh-Hip Injury Criterion (KTHIC), mais son utilisation est réservée aux modèles humains.

Il est défini par :

 

t<21ms : f=a-b*te	avec a=23.4 kN, et b=0,72 kN/ms
t=21ms : f=8.3 kN

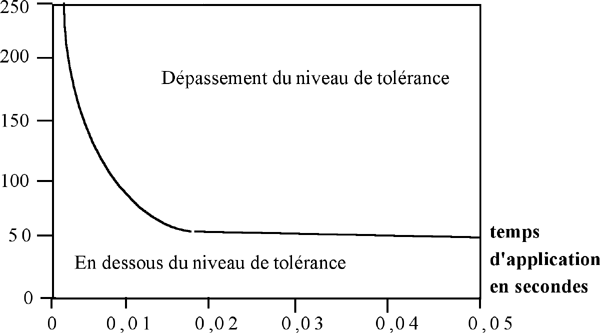
où te est la durée de la pulsation conventionnelle, définie par :

où t est la durée totale de l'impulsion.

 

La forme de ce second critère ressemble à celle du FIC de Viano, mais la base temporelle est différente. En appliquant le FIC aux résultats des tests de Leung, celui-ci paraît plus optimiste que le critère KTHIC.

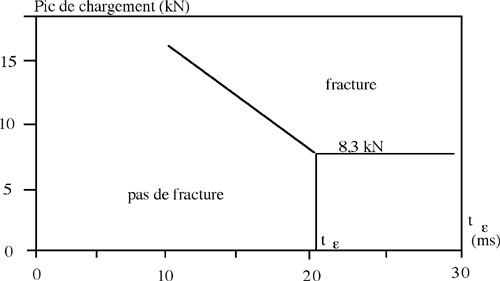
Pic de la force d'impact sur le genoux fonction de la durée conventionnelle de pulsation.

Citons enfin un dernier critère pour cette partie du corps, trouvé dans un article de Mertz datant de 1991, et proposé à l'Organisation Internationale de la Normalisation (ISO/TC22/SC12/WG5/N312). La définition de ce critère est particulièrement adaptée pour les mannequins. Le critère permet de vérifier si la durée d'application d'un effort axial, réparti sur le genou est en dessous d'un seuil.

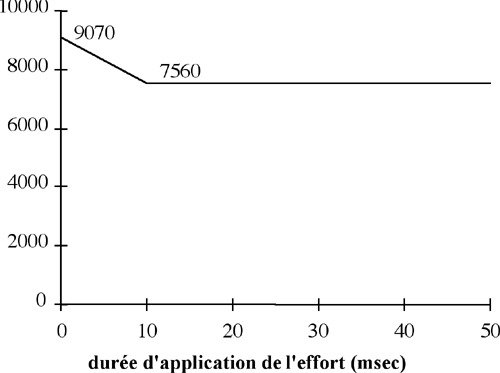
Critère dépendant du temps pour le chargement du fémur.

 

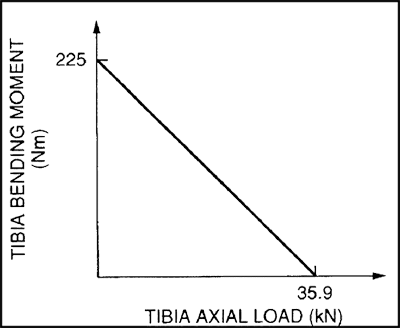
Le critère proposé en ce qui concerne le tibia est un effort limite de 1800lbs qui tient compte des moments de flexion et des forces de compression. Le NHTSA (National Highway Traffic Safety Administration) a proposé d'adopter le critère décrit par la formule suivante :

 

M / Mc + P / Pc < 1

 

Où :

Mc = 168 lbs-ft
Pc = 7.950 lbs
M et P sont les moments et les forces de compression mesurés.

 

 Si la somme des ratios des moments de flexion aux deux extrémités du tibia (genou et cheville) et de la force de compression est inférieure à 1, des fractures du tibia ou du fibula ne devraient pas se produire.