Les principes de la modélisation
La modélisation est basée sur l'utilisation des réseaux de Petri pour représenter le système, et plus particulièrement ses 4 sous-systèmes :
-
Le sous-système Bâtiment ;
-
Le sous-système « occupants » ;
-
Le sous-système « service d'intervention » ;
-
Le sous-système « environnement ».
Le sous-système Bâtiment repose sur deux notions de base, les locaux et les équipements.
-
Par local , nous considérons toute partie élémentaire du bâtiment pouvant constituer une entité vis à vis de l'incendie. Un local peut donc être tout aussi bien une pièce, un couloir, un escalier ou même une gaine technique.
-
Un local peut même regrouper différents locaux si nécessaire. Ainsi, plusieurs locaux de type « pièce » peuvent-ils être regroupés pour constituer un local de niveau géométrique supérieur, appelé « zone ».
Il est ainsi possible de constituer des entités plus vastes dont les éléments ont un comportement commun. Cela est très intéressant pour caractériser, par exemple, des zones thermiques ou acoustiques. Il est ainsi possible de constituer une zone thermique « Nord » dont les équipements et le comportement thermique seront différents de ceux d'une zone thermique « Sud ». Même si la configuration géométrique est identique par exemple, les équipements seront certainement différents et le comportement de chaque zone devra être séparé. Cette notion de zone peut aussi être utilisée pour la sécurité incendie pour, par exemple, regrouper des locaux d'un même étage dotés d'équipements d'alarme ou de sécurité similaires. Pour de vastes bâtiments, la notion de zone permet aussi de réduire le nombre d'entités volumiques à considérer et par conséquent, le nombre des interfaces entre ces entités.
-
La notion d'équipement d'un local fait référence à tout système technique ou constructif pouvant avoir une influence sur le déroulement de l'incendie. Les ouvertures d'un local de type « pièce », portes et fenêtres, sont considérées comme des équipements puisque leur comportement dans le temps sous l'effet de l'incendie influence le déroulement ainsi que leur manipulation par les occupants, portes et fenêtres ouvertes ou fermées. Les gaines de ventilation dans un couloir sont considérées comme un équipement de ce local. Les gaines verticales pourront être considérées comme des locaux en tant que tels ou comme un équipement d'un local de type « cage d'escalier ». Le choix entre les deux solutions est laissé à l'appréciation de l'utilisateur, mais dépend aussi du positionnement géométrique de la gaine technique considérée.
La modélisation par les réseaux de Petri (RdP) est donc basée sur les quatre principes complémentaires suivants :
-
Des réseaux de Petri élémentaires permettant de décrire les différents éléments d'un sous-système;
-
La communication entre ces réseaux élémentaires
-
des modèles de calcul des grandeurs physiques liées à l'incendie.
-
Un assemblage des réseaux élémentaires pour reconstituer le modèle du projet étudié.
Un modèle est donc constitué de nombreux réseaux de Petri élémentaires (RdPE) et indépendants décrivant chacun le comportement vis à vis de l'incendie d'un équipement ou décrivant l'état d'un local. Il est ainsi possible de proposer des RdPE génériques décrivant une fois pour toutes le comportement de tel ou tel équipement dans tous les cas. Ces RdPE génériques sont considérés comme des blocs qui peuvent être ensuite instanciés pour décrire le comportement d'un équipement particulier de même nature.
Ainsi, le même RdPE générique « porte » permettra de décrire toutes les portes d'un même local de type « pièce » par exemple.
D'autres RdPE sont construits pour décrire les autres sous-systèmes intervenant dans la sécurité incendie. Il s'agit par exemple de RdPE construits pour décrire les équipements de sécurité et/ou de détection ou le système d'alarme. Ce sont aussi des RdPE construits pour décrire les conditions d'intervention du service de secours ou le comportement des occupants. Ces différents RdPE peuvent être modélisés de façon plus ou moins fine selon les connaissances que les acteurs sont capables de formaliser et selon leur fiabilité.
La connexion indispensable entre les différents RdPE pour décrire correctement le développement d'un événement incendie s'effectue par le biais de messages qui sont échangés entre les différents RdPE concernés. Ces messages portent sur l'état d'un local vis à vis de l'incendie ou sur le comportement de tel ou tel équipement qui conditionne alors la propagation de l'incendie. Le comportement d'un équipement se traduit en fait par des changements d'état du système qui sont susceptibles d'entraîner un déroulement différent de la propagation de l'incendie. L'état des composants ou des équipements ne peut être correctement évalué qu'au travers de grandeurs physiques comme la température ou la hauteur de fumée dont les valeurs conditionnent les messages envoyés dans les RdPE et leurs transitions, c'est à dire les changements d'état qui en résultent. Ainsi, par exemple, la destruction par pyrolyse d'une porte entre deux locaux peut être constatée si la température de la zone chaude dans l'un des deux locaux atteint une valeur donnée pendant un temps suffisant. Il est ainsi nécessaire de connaître à chaque instant la température de la zone chaude de fumée et la hauteur de cette zone chaude.
La hauteur de la zone chaude de fumée et la température de cette zone chaude doivent être calculées dans chaque local. Des modèles multizones relativement complexes ont été construits historiquement par le CSTB et d'autres organismes pour évaluer les paramètres de l'incendie et leur évolution dans le temps. Ces modèles sont complexes et nécessitent des temps de calcul importants même avec les ordinateurs rapides actuels.
Mais il est aussi possible d'utiliser des modèles simplifiés, plus rapides, basés sur des hypothèses plus basiques permettant de décrire plus facilement un comportement approché des fumées et d'évaluer des températures de fumée. En effet, l'évaluation rapide des grandeurs physiques (hauteurs de fumée, températures) est un impératif absolu si l'on veut maintenir l'objectif d'évaluer les dommages potentiels d'un incendie par la simulation de très nombreux scénarios d'incendie différents par les RdP dans des temps de calcul raisonnables.
Sans entrer dans le détail, les comparaisons menées par Julien Chorier au cours de sa thèse montre que des modèles simplifiés apportent des résultats très comparables aux modèles de calcul complexe pour cette approche.
Cet aspect concerne surtout le système bâtiment qui s'avère très complexe à décrire.
Les différents RdPE peuvent être regroupés pour décrire les relations entre les « objets » du bâtiment. Il est ainsi possible de traduire la géométrie du bâtiment et la disposition des pièces les unes par rapport aux autres, ainsi que les composants et équipements présents dans chacune d'elle.
Le lecteur trouvera une abondante littérature sur les réseaux de Pétri.
Les réseaux de Petri sont largement utilisés pour la modélisation et l'analyse de systèmes à événements discrets. Ce succès est dû à de nombreux facteurs. Parmi ceux-ci, nous pouvons relever leur simplicité de compréhension, leur nature graphique se prêtant sans grande difficulté à la modélisation de phénomènes complexes, et la possibilité de disposer d'un arsenal de résultats mathématiques analytiquesGrolleau, E., A. « Choquet-Geniet, et al. (1999). Modélisation de systèmes temps réel par réseaux de Petri autonomes en vue de leur analyse hors-ligne, Modélisation des Systèmes Réactifs, MSR'99. Cachan, France, Hermes. »
Le fichier suivant est un extrait de la thèse de Julien Chorier.
L'outil utilisé pour modéliser les systèmes (Logiciel MOCA-RP v12) offre quelques possibilités supplémentaires par rapport aux réseaux de Pétri de base.
Un réseau de Petri, est défini classiquement par :
-
un graphe ;
-
formé de deux types de nœud appelés places et transitions reliés par des arcs orientés
-
et biparti, c'est-à-dire qu'un arc relie alternativement une place à une transition et une transition à une place ;
-
composé de jetons qui passent d'une place à l'autre par l'intermédiaire d'une transition. On retrouve ces éléments sur la Figure suivante.
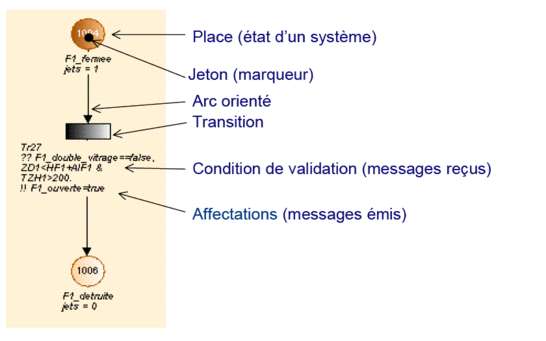
On peut aussi rappeler que les places correspondent à un état du système et que les transitions sont définies par trois paramètres :
-
Des gardes, conditions à remplir pour que le délai de la transition puisse démarrer (condition de validation) ;
-
Un délai, qui une fois écoulé permet la validation de la transition et le passage du jeton à la place suivante et donc du système à l'état suivant ;
-
Des affectations, messages émis. Ces affectations ont lieu, en parallèle, après le tir de la transition et consistent en une liste de couple (variable, expression).
L'état initial du système est défini par le marquage initial des places. Certaines places d'entrée sont marquées quel que soit le cas particulier traité, d'autres places peuvent contenir ou ne pas contenir de jetons. Elles permettent de valider des options de simulation (défaillances de matériels de détection, pièce vide, ...). Elles sont validées avant le lancement d'une simulation. Dans la description d'une transition il est possible de spécifier une liste d'expressions booléennes qui doivent être nécessairement vérifiées pour que la transition soit valide. Ces expressions sont séparées par des virgules. Il s'agit des conditions de validation. Le message émis introduit une liste d'affectations de variables. Ces affectations ont lieu, en parallèle, après le tir de la transition et consistent en une liste de couple (variable, expression) où variable et expression sont du même type. Toutefois, il est important de préciser qu'il n'est pas possible d'affecter un nombre de jetons à une place et que les variables sont affectées avant la production de jetons.
Pour représenter les réseaux de Petri et réaliser nos simulations, nous avons utilisé le logiciel MOCA-RP. Le logiciel MOCA-RP (MOnte-CArlo basé sur les Réseaux de Petri) est destiné à la simulation du comportement des systèmes dynamiques complexes dans le but d'obtenir, par un traitement statistique, des résultats concernant leur fiabilité, disponibilité, productivité, ainsi que tout autre paramètre probabiliste.
Le modèle du système à étudier est réalisé sous la forme d'un réseau de Petri stochastique interprété qui sert de support à une simulation de Monte-Carlo classique.
En 2002, une collaboration entre Total-Fina-Elf et la société IXI-GFI Consulting a conduit au développement de la version 12 du logiciel MOCA-RP. Cette version intègre principalement, les messages et états statistiques complexes, la possibilité d'intégrer des lois spéciales en langage C et permet aussi de thésauriser des modèles RdPS au sein de bibliothèques pour faciliter leur réutilisation par des ingénieurs non spécialistes des Réseaux de Petri.
MOCA-RP gère des lois de transition différentes pour calculer le temps de séjour dans une place amont lorsque la transition est dite sensibilisée ou franchissable. Durant ce délai, la transition doit être sensibilisée en permanence pour être tirée. Certaines de ces lois sont des lois dites à mémoire, c'est-à-dire que le temps passé dans une place n'est pas remis à zéro si la sensibilisation de la transition est interrompue avant franchissement. Cette valeur est reprise lorsque la transition est de nouveau sensibilisée. La loi dite "défaillance à la sollicitation" est une loi spécifique à MOCARP qui ne respecte pas la règle de tir d'une transition des réseaux de Petri "classiques". En effet, la règle consiste normalement à retirer un jeton dans chacune des places amont et à mettre un jeton dans chacune des places en aval. Dans le cas du tirage de ce type de transition particulier à MOCARP, on retire un jeton dans chacune des places amont et l'on met un jeton dans la place aval choisie aléatoirement en respectant les "proportions" γ pour la place représentant la défaillance à la sollicitation et (1 - γ) pour la place représentant la non défaillance lors de la sollicitation.
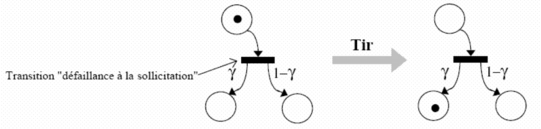
En général, la place amont correspond à l'état "attente" du composant, l'une des places aval correspond à l'état "panne" du composant et l'autre à l'état "fonctionnement". γ est la probabilité de défaillance à la sollicitation d'un composant en attente ou en d'autres termes le nombre de chances de voir le composant refuser de fonctionner lorsqu'on le sollicite. Le délai associé au franchissement de ce type de transition est nul. Lorsque l'utilisateur ne trouve pas la loi de transition qui lui convient, parmi les lois fiabilistes actuellement implémentées dans MOCA-RP (exponentielle, log-normale, Weibull, Dirac ...), il lui est possible de programmer lui-même sa propre loi.
