Variables aléatoires continues
Soit X une variable aléatoire réelle, la loi de probabilité de X est définie par une fonction de répartition PX(x) telle que :
Si PX est dérivable, sa dérivée pX est la densité de probabilité de X telle que :
Et :
Moments d'une variable aléatoire
L'espérance mathématique est le moment d'ordre 1, soit la moyenne pondérée :
La variance est le moment centré d'ordre 2, dont la racine carrée est l'écart-type, mesure de la dispersion de X autour de son espérance :
Les moments centrés d'ordre supérieur permettent de caractériser la dissymétrie de la distribution autour de la moyenne (ordre 3) et son aplatissement (ordre 4).
Quelques lois de probabilité univariées
Les quelques lois de probabilité données ici sont parmi les plus utilisées dans les applications courantes en fiabilité des structures de génie civil.
La loi normale (de Laplace-Gauss) est la loi la plus utilisée car elle représente bien la variabilité de nombreux phénomènes naturels, sa densité de probabilité est :
Des grandeurs telles que le poids volumique des matériaux ou la hauteur de neige présentent ce type de distribution. Pour une variable normale centrée réduite N(0,1), , la fonction de répartition devient la fonction complémentaire d'erreur :
La loi lognormale (de Galton) décrit la variabilité de grandeurs positives, dont le logarithme suit une loi normale, sa densité de probabilité est :
Les propriétés mécaniques ou de transfert des matériaux présentent souvent cette distribution, de même que les grandeurs géométriques des sections ou des éléments de structure.
La loi uniforme, appelée aussi loi des hasards, est utilisée lorsque toutes les valeurs de X sont équiprobables dans un intervalle donné [a,b] avec une probabilité égale à (b-a)-1. Cette loi est donc bornée :
Cette loi permet notamment de modéliser des aléas provenant d'une usure répétée d'outils. Prenons le cas d'un foret destiné à réaliser un perçage unique dans chaque pièce. Si l'usure est régulière et le remplacement de l'outil réalisé périodiquement, le diamètre de perçage suivra une distribution uniforme.
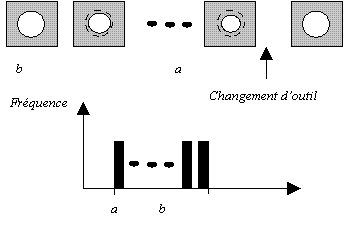
Il peut en aller de même d'un coffrage dont le cadre en acier se plastifie peu à peu.
La loi uniforme joue également le rôle de loi dite non informative, utile lorsque l'on ne connaît que la plage de variation finie possible d'une variable, l'observation de la variable ne permettant pas de dire qu'elle a plus de chance de tomber dans un intervalle donné que dans un autre, de même ouverture. Le manque de données d'observation peut également conduire au choix de la loi uniforme.
Waloddi Weibull (1939) a proposé la loi du même nom pour représenter la distribution de résistances à la rupture de matériaux. La loi de Weibull est une généralisation à deux paramètres de la loi exponentielle qui a pour densité :
Sa fonction de densité de probabilité s'écrit :
est donc .
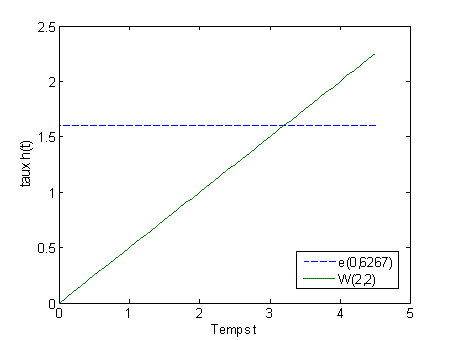
Outre son usage initial (distribution de résistances à la rupture), cette loi permet notamment de modéliser des durées de variables aléatoires et est donc particulièrement utile en fiabilité (sans défaillance, ni réparation). Dans cette perspective, elle est d'utilisation plus souple que la loi exponentielle. Pour illustrer ce point, considérons le taux de rupture instantané h(t) appelé aussi taux de risque («hazard rate» en anglais). Ce taux s'écrit :
où f(t) et F(t) sont la fonction de densité de distribution et la fonction de répartition de la rupture à un instant t. correspond à un matériel qui se dégrade avec le temps (usure) ; correspond à un matériel qui se bonifie avec le temps ; (loi exponentielle) correspond à un matériel sans usure (pannes accidentelles).
Il s'agit du taux instantané de défaillance à l'instant suivant t de survivants à l'instant t. Son unité est en général le [nombre de défaillances / unité de temps]. Il s'agit d'une probabilité conditionnelle puisqu'au dénominateur, on retrouve la probabilité de non défaillance. Si on considère alors pour f(t) et F(t) les fonctions correspondant à une loi exponentielle, h(t) est constant alors qu'il varie si la loi est une loi de Weibull, ce qui est une hypothèse plus réaliste. La figure ci-dessous illustre ce cas.
Lorsque les données présentent nécessairement des bornes (grandeurs positives comme les résistances, grandeurs bornées comme les enrobages), l'utilisation de lois de probabilité à domaine borné se révèle indispensable. Bien que n'importe quelle loi de probabilité puisse être définie entre deux bornes, par l'intermédiaire de troncatures, il peut s'avérer plus séduisant de recourir à des lois naturellement bornées, comme la loi log-normale ou la loi bêta, hormis la loi uniforme, qui reste assez pauvre. La loi bêta présente par ailleurs l'avantage de bénéficier de paramètres de forme : ces derniers permettent de donner à la loi bêta une forme proche d'autres lois.
La densité de probabilité de la loi bêta s'écrit :
où sont les paramètres de forme positifs, a et b les bornes de variation avec a≤x≤b, est la fonction gamma, soit . et . Les Figure 3a et 3b illustrent la «souplesse» de la loi bêta, ici sur l'intervalle [0,1].
![Figure 3a : Loi bêta (5,5) sur l'intervalle [0,1].](../res/Quantitatif_figure3a.png)
![Figure 3b : Loi bêta (3,8) sur l'intervalle [0,1].](../res/Quantitatif_figure3b.png)
Les processus stochastiques variables dans le temps et/ou dans l'espace ne peuvent généralement pas être décrits par des lois de probabilité univariées. Cependant, lorsque l'on ne s'intéresse qu'à une caractéristique de ces processus, comme par exemple leurs valeurs extrêmes (valeurs extrêmes de hauteur de neige sur les toitures, de vitesse de vent, de hauteur de houle, de charges sur les ponts, valeurs de hauteur de crue), des lois univariées sont fréquemment employées. Citons plus particulièrement la loi de Gumbell et la loi de Fréchet dites à valeurs maximales.
-
La densité de probabilité de la loi de Gumbel s'écrit :
où et .
-
La densité de la loi de Fréchet s'écrit :
où u est le paramètre de position avec u>a, a la borne inférieure avec x≥a et le paramètre de forme avec , et .
Les lois qui suivent sont particulièrement utilisées dans l'inférence statistique.
Si U1, ..., Un sont des variables normales centrée réduites et indépendantes, la variable suit la loi du khi2 à n degrés de liberté, de densité de probabilité :
Si U, U1, ..., Un sont des variables normales centrées réduites et indépendantes, la variable suit la loi de Student à n degrés de liberté, de densité de probabilité :
