Les capacités de simulation numérique sont directement dépendantes des performances des ordinateurs
La simulation numérique permet de reproduire sur un ordinateur un phénomène complexe que l'on souhaite étudier et prédire. Cette expérience numérique repose sur des modèles théoriques qui sont formulés par des lois mathématiques... des lois mathématiques qu'il convient d'évaluer numériquement à chaque instant et en tout point de l'espace sur la totalité du domaine d'étude. Comme il y a une infinité de valeurs à calculer, cet objectif est inaccessible : c'est pourquoi, pour des raisons de faisabilité, il est admis de ne considérer qu'un nombre fini de points en discrétisant l'espace d'étude. Le nombre d'opérations à effectuer devient alors abordable pour un ordinateur.
Cette discrétisation[1], qui repose souvent sur un maillage[2][2] de l'espace, est le résultat d'un compromis entre :
l'utilisation d'une discrétisation[1] la plus fine possible pour « coller » au mieux à la réalité
l'utilisation d'une discrétisation la moins raffinée possible pour diminuer le nombre des calculs à effectuer et donc accélérer la rapidité de la simulation.

Exemple :
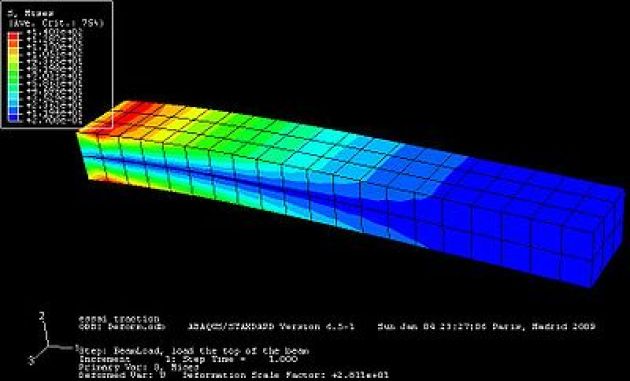
L'exemple ci-dessous illustre bien l'importance du choix de la discrétisation. L'étude porte sur une poutre encastrée chargée ponctuellement en son extrémité. La théorie de la résistance des matériaux donne, pour ce cas particulier, une contrainte maximale de 400Mpa et une flèche de 10,6mm.

Une étude mécanique est menée via le logiciel CATIA V5 pour différents maillages (i.e. discrétisation du volume de la poutre. Les résultats sont comparés en fonction de leur consommation en ressource informatique (temps CPU, RAM, ...) et de leur qualité, c'est à dire de leur proximité avec le résultat de la RDM[3].
Taille (mm) | Temps (s) | Ram (Ko) | Swap (Ko) | Déf. (mm) | Erreur déf. (%) | Contrainte (MPa) |
|---|---|---|---|---|---|---|
25 | 0,01 | 51 | 22 | 3,23 | 70 | 146 |
10 | 0,05 | 119 | 63 | 6,25 | 41 | 245 |
2 | 0,1 | 597 | 618 | 8,04 | 24 | 321 |
2,5 | 1 | 2200 | 4180 | 10,3 | 3 | 378 |
1,5 | 10 | 6440 | 21800 | 10,6 | 0 | 392 |
1 | 200 | 21400 | 140000 | 10,6 | 0 | 400 |
On constate donc que pour obtenir un calcul précis (erreur de 3%) il faut discrétiser la poutre avec au minimum un point tous les 2,5mm. Ce calcul est effectué par la machine en une seule seconde. Pour obtenir un calcul plus précis (erreur < 0,1%), il faut raffiner le maillage (un point tous les millimètres). Mais alors, l'ordinateur met 200 fois plus de temps pour effectuer le calcul. On imagine que pour des modèles plus complexes, comme celui d'un bâtiment complet, le choix de la discrétisation est primordial : puis-je effectuer un calcul suffisamment précis dans un temps raISO[4]nnable ?