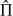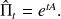Représentation Canonique
Comme en temps discret, on partitionne l'espace d'état, E, en deux parties :
Cela permet de représenter le générateur infinitésimal sous une forme canonique simple. Pour ce faire on rassemble les états par classe et on ordonne les classes selon si elles sont finales ou transitoires. On aboutit à la représentation suivante : | 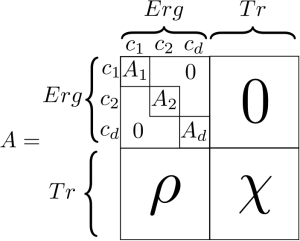 Générateur infinitésimal sous forme canonique |
On obtient ainsi de même la matrice de transition associée à la chaîne discrète
| 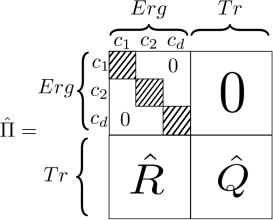 Matrice de transition canonique associée |
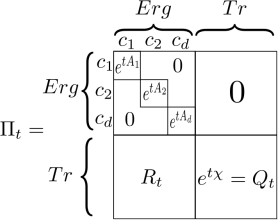
Matrice des probabilités à tout instant