Chaîne discrète associée
Si on note
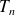les instants de transition, la chaîne discrète associée au processus
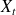est la chaîne
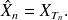
Elle a pour matrice de transition
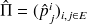avec :
si i non absorbant :
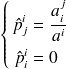
si i absorbant :
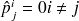
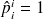
Le diagramme de transition de la chaîne en temps continu,
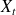, est celui de la chaîne discrète associée
.
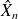Remarque :
Le diagramme de transition correspondant à celui de la chaîne discrète associée, les notions de classification des états restent les mêmes.
On retrouve donc les mêmes représentations d'état ergodique, des états transitoires, des classes finales etc... mais pas les notions de périodicité. L'absence des notions de périodicité est due au fait que désormais le temps entre deux transitions n'est pas fixe, il ne s'agit plus simplement d'une itération. On peut donc retrouver les phénomènes périodiques des chaînes discrètes sauf qu'ils ne correspondent plus à des périodes de temps fixe. De plus, on redéfinit les opérateurs sur les états et les classes vus dans le cadre des chaînes discrètes pour les généraliser aux chaînes à temps continu.
Définition :
On note
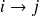,si et seulement si
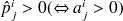ce qui signifie que l'on peut passer de l'état i à l'état j en une transition.
On note de même
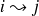si et seulement si
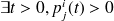, ce qui signifie qu'il existe un chemin qui mène de l'état i à l'état j.
