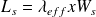Loi de Little
Définition : État d'un système
Nous appelons état d'un système à l'instant t le nombre n(t) de clients présents dans le système à cet instant (un client est "présent dans le système" si il est en file d'attente ou en cours de service). Les quantités fondamentales auxquelles s'intéresse l'analyste dans le cadre des modèles de files d'attente sont les probabilités d'état, que nous définissons de la façon suivante : pour n=0,1,.... et t>=0,
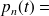probabilité que n clients soient présents à l'instant t dans le système.
Sous certaines conditions, les probabilités à long terme ou probabilités stationnaires existent pour n=0,1,... On interprète alors
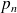comme la probabilité que, à un instant quelconque dans le long terme, exactement n clients soient présents dans le système.
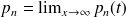
Lorsque ces probabilités sont connues, on a la possibilité de calculer de nombreuses mesures de performance du système de files d'attente. Les plus importantes sont les suivantes :
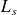= nombre espéré de clients dans le système ( à un instant quelconque dans le long terme).
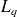= nombre espéré de clients dans la file d'attente.
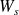= temps espéré passé par chaque client dans le système.
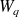= temps espéré passé par chaque client dans la file d'attente.
Par définition on a :
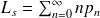
De plus, si le système comporte c serveurs parallèles, alors
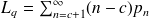
Loi de Little
La relation entre les paramètres L est W est un peu plus compliquée, néanmoins jouant un rôle très important dans la théorie des files d'attente. Introduisons alors
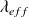représentant le taux d'entrée moyen des clients dans le système (nombre moyen de clients entrant dans le système par unité de temps). La relation liant toutes ces données s'appelle loi de Little et est définie par :
