Loi des arrivées
Dans la suite de ce cours, nous allons considérer que nous sommes en présence d'une file d'attente ponctuée par un service. Nous savons que ces files sont caractérisées par le fait que le temps des services ont une durée qui suit une loi Exponentielle et que le nombre d'unité admises dans la file suit une loi de Poisson. Dans la suite de ce cours, nous allons nous appliqué à décrire ces deux lois à l'aide de la théorie mathématique ainsi qu'à l'aide de petits exercices.
Définition : Processus de Poisson
Un processus de comptage
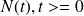 est un processus de Poisson avec paramètre
est un processus de Poisson avec paramètre
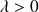 si
si
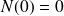
Les incréments de
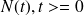 sont indépendants
sont indépendantsLe nombre d'événements dans l'intervalle
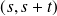 obéit à la loi de Poisson :
obéit à la loi de Poisson :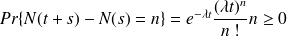
L'expérience montre que généralement, le nombre d'arrivées dans une file d'attente suit une loi de Poisson. La probabilité précédente représente donc la probabilité de réalisation de n événements pendant la durée t+s. Dans le cadre des files d'attente, cette loi nous permet donc d'estimer la durée entre deux arrivées consécutives.
Loi de Poisson
Dans cette partie, nous avons représenté la loi de poisson sous forme d'applet.
En noir on a la densité de la loi de poisson, alors que en bleu on a la fonction de répartition de la même.
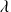 est le parametre de la loi et kmax représente la valeur de x ou on s'arrête.
est le parametre de la loi et kmax représente la valeur de x ou on s'arrête.





