Actualisation des paramètres d'une loi de distribution
L'actualisation des paramètres des lois de distribution (estimateurs statistiques : moyenne, variance) peut-être basée sur deux types d'inférence : l'inférence statistique classique et l'inférence bayesienne. La première a déjà été présentée brièvement dans les sections précédentes, et s'appuie généralement sur des données suffisamment nombreuses pour revêtir une signification statistique probante. Dans le cas où les données sont peu nombreuses, l'inférence bayesienne constitue un outil pertinent.
Inférence bayesienne
Si représente le paramètre inconnu ( ), auquel on conditionne la loi de distribution des observations disponibles indépendantes x={x1,..,xn}, la fonction de vraisemblance de s'écrit
La loi a priori concentre les informations disponibles sur . La formule de Bayes permet alors d'exprimer
où est la loi a posteriori du paramètre où est la loi a posteriori du paramètre , une fois prises en compte les observations x. La loi de distribution p(x) est la loi marginale de x, soit
Le formalisme bayesien est assez simple, mais les calculs analytiques deviennent rapidement inextricables et impliquent des choix judicieux de la loi a priori de et de la loi jointe de , qui conduisent à une loi a posteriori connue (on parle de lois conjuguées). Si les lois a priori ne sont pas disponibles ou/et si p(x) n'est pas directement calculable, on doit recourir à des formulations numériques reposant notamment sur l'algorithme de Gibbs et sur les méthodes de chaînes de Markov par simulations de Monte Carlo (méthodes dites MCMC, voir le site du logiciel Winbugs : http://www.mrc-bsu.cam.ac.uk/bugs/welcome.shtml).
Actualisation de la moyenne d'une distribution normale de variance connue
Le paramètre inconnu de la loi de distribution de x est ici la moyenne , alors que sa variance est supposée connue. On suppose également que chaque observation xi suit une loi normale conditionnée à
Si l'on suppose que suit une loi uniforme entre et (loi a priori non informative), alors on trouve que , où mX est la moyenne des observations x, suit une loi normale tronquée entre et
Si l'on suppose que suit une loi normale de moyenne et de variance (loi a priori informative), alors on trouve que , où mX est la moyenne des observations x, suit une loi normale de moyenne et de variance
Ouvrages généraux :
Droesbeke J. J., Fine J., Saporta G. "Méthodes bayésiennes en statistique", Editions Technip, 2002.
Actualisation de la variance et de la moyenne d'une distribution normale
Les paramètres inconnus de la loi de distribution de x sont ici la moyenne et la variance . Si l'on dispose de mesures antérieures aux observations actuelles, caractérisées par un nombre de mesures n0, les estimateurs sans biais m0 pour la moyenne et s02 pour la variance, on peut proposer une loi conjointe a priori de , conditionnée à ces mesures. suit une loi normale conditionnée à la fois à et aux mesures :
Puisque la variable , avec , suit la loi du khi2 à dégrés de liberté, la variable , conditionnée à et s02, suit la loi gamma (la loi du khi2 est un cas particulier de la loi gamma), et son inverse suit la loi gamma-inverse
En omettant dans l'écriture le conditionnement aux mesures antérieures (l'origine de l'information a priori), on obtient la loi jointe a priori, qui est ici la loi normale-gamma-inverse d'ordre 1 (dimension de la variable normale) :
La fonction de vraisemblance peut s'obtenir par simple décomposition, étant donnée l'indépendance de mX et sX2 :
avec
si n est nombre d'observations, et
On peut alors écrire formellement la loi jointe a posteriori de
On trouve qu'il s'agit à nouveau d'une loi normale-gamma-inverse d'ordre 1, dont on tire les espérances et variances a posteriori de et :
avec
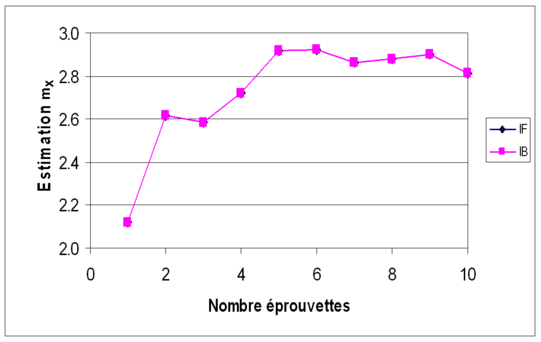
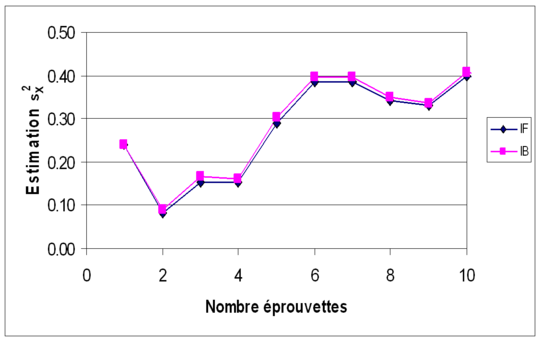
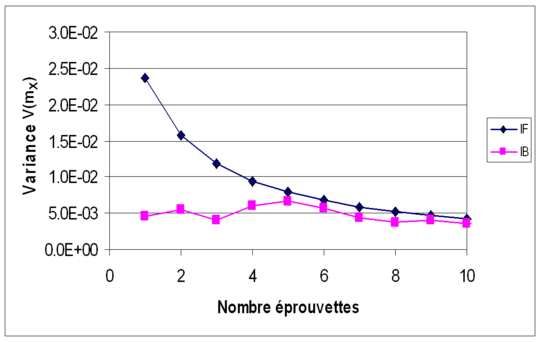
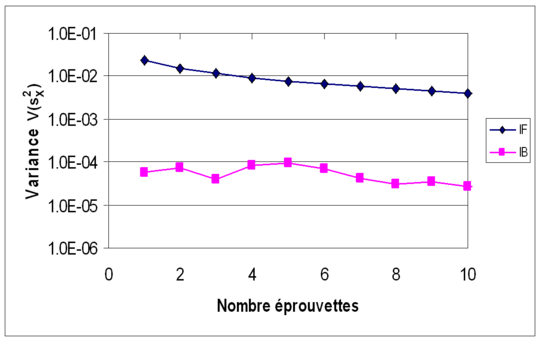
Les données utilisées auparavant (Exemple 4 et Exemple 5) sont à nouveau considérer. Les figures suivantes (Figures 7a, 7b, 7c et 7d) montrent l'évolution, en moyenne et en variance, des estimateurs mX et sX2 en fonction du nombre d'éprouvettes testées (nombre de données) ; l'inférence classique (ou fréquentiste) est notée IF, l'inférence bayesienne est notée IB. Sur les deux premières figures (moyennes de mX puis de sX2), on voit que les résultats diffèrent peu. La différence est plus sensible sur les deux dernières figures (variances de mX puis de sX2), où l'on voit que l'approche bayesienne permet de réduire l'incertitude sur les estimateurs statistiques.