Les propriétés descriptives des concepts (aussi appelées attributs)
Nous en avons déjà examinée une : l'identifiant, qui est une propriété particulière.
Par exemple, pour le concept « enseignant », c'est son « nom ».
Mais on peut associer autant d'informations qu'il est nécessaire à une classe, pour les besoins d'une procédure.
Par exemple, pour l'enseignant, il faut savoir son numéro de sécurité sociale, son adresse, sa date de naissance, sa nationalité, ses diplômes, s'il est marié, s'il a des enfants, s'il a d'autres activités, la puissance de sa voiture ... toute information qui sera exploitée pour des tâches administratives (fiche de paye, remboursement de frais), pédagogiques (affectation), et peut être d'autres encore ...
En général, on donne le statut de « propriété[1] » à toute information qui ne fera sans doute pas l'objet d'un concept ou d'une relation. C'est une information « terminale » et son statut dépend du contexte. Par exemple, si le fait d'être marié implique que l'on doive connaître avec qui, alors on est obligé de développer une idée, ou relation, dont le rôle devient « est marié (e) avec ».
On représente une propriété (ou plusieurs) de la manière suivante :
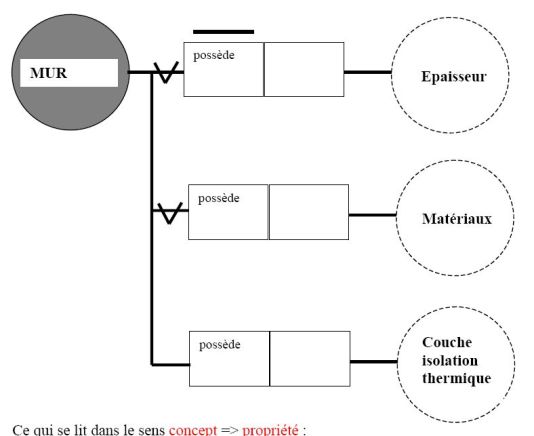
Ce qui se lit dans le sens concept[2] → propriété[1] :
Tout mur ( sous-entendu morceau de mur homogène) possède
une seule épaisseur
zéro, un ou plusieurs matériaux (zéro pour une paroi virtuelle)
Un mur peut avoir une isolation thermique (autre façon de dire un mur a zéro, une ou plusieurs couches d'isolation thermique)
Dans l'autre sens, on ne dit rien, car il n'y a pas d'ambiguïté possible.






