Pour mémoire, classification ensembliste des relations binaires entre concepts
Pour l'instant, nous n'avons pas donné de nom aux relations entre concepts.
Leur nature sémantique, nous avons vu qu'elles étaient « binaires » du point de vue mathématique, dépend de la signification donnée par l'utilisateur. Selon les cas, ce seront des relations de proximité, de voisinage, de décomposition, d'appartenance, d'affinité, de correspondance ... La liste est illimitée, ouverte.
La seule propriété commune de ces relations binaires est de mettre « en correspondance » certains objets de l'ensemble A avec ceux de l'ensemble B.
Si l'on veut être plus précis sur une classification de la nature structurelle de ces relations, on peut faire appel aux propriétés identifiées en algèbre ensembliste, qui distingue par exemple 8 cas possibles issus de la combinatoire des contraintes appliquées aux relations binaires entre deux ensembles (en éliminant les symétriques) :
l'injection
la bijection
la surjection
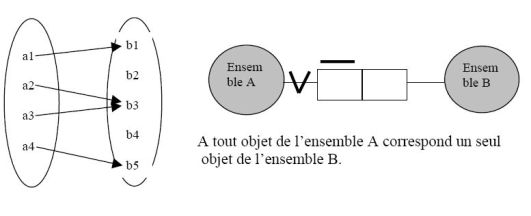
l'application simple
la fonction
la relation 1-N
la relation 1-1
la relation N-M
On peut représenter chaque relation ensembliste par un schéma NIAM, et inversement chaque idée d'un schéma NIAM peut être qualifiée par une relation ensembliste.
A titre d'exercice, pour ceux qui n'ont pas oublié leurs cours de mathématiques du primaire ou du secondaire, vous pouvez vous amuser à reproduire les schémas des 8 relations ensemblistes citées plus haut.
Par exemple, le schéma de « l'application simple », accompagné de son diagramme de Venn.