Les idées
Ce terme est utilisé pour exprimer une relation[1] entre deux concepts[2], A et B par exemple.
N'oublions pas qu'un concept s'identifie à un ensemble.
Une idée[3] est donc une relation ensembliste, c'est à dire qu'elle permet de mettre en relation un certain nombre d'objets de l'ensemble A avec ceux de l'ensemble B, et inversement, car une relation entre A et B peut se lire dans les deux sens.
La nature sémantique de la relation n'est pas formalisée, c'est seulement ses propriétés qui le sont, à travers des contraintes[4] binaires de cardinalité.
Un exemple, tiré du cours de H. Habrias[5] qui se propose de modéliser les données d'une école. Commençons par exprimer une idée entre les deux concepts « enseignant » et « matière ».
Au départ, avant toute réflexion sur les contraintes[4], on met en place le vocabulaire syntaxique composé des concepts, avec ou sans les identifiants, et des rôles[6], pour lesquels on peut formuler un petit texte (prédicat) pour fixer les idées (l'idée !).
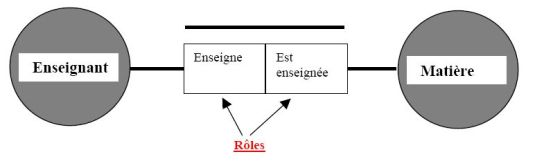
Si on n'impose aucune contrainte de cardinalité sur la relation (ce qui est noté par le trait épais couvrant les deux rôles) et qu'on laisse le schéma en l'état, on le traduit en langue naturelle par les deux phrases élémentaires[7] suivantes :
Dans le sens "enseignant" => "matière" :
Zéro, un ou plusieurs "enseignants" enseignent zéro, une ou plusieurs "matières".
Dans le sens "matière" => "enseignant" :
Zéro, une ou plusieurs "matières" sont enseignées par zéro, un ou plusieurs "enseignants".
En effet, sans contrainte[4] de cardinalité, toutes les éventualités sont possibles !






