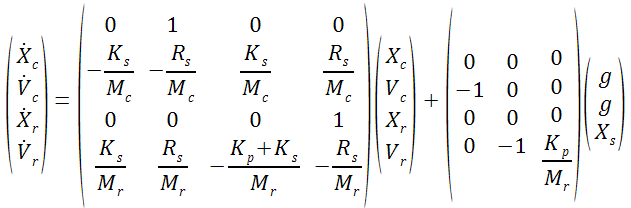Recherche des valeurs propres du modèle monoroue
Les valeurs propres d'un système vibratoire représentent ses dynamiques internes ; ce sont des caractéristiques intrinsèques au système. Elles forment les différentes réponses libres, ce que l'on appelle plus couramment la réponse transitoire du système.
Recherche des valeurs propres avec AMESim
Le logiciel AMESim est en mesure de calculer numériquement les valeurs propres d'un système vibratoire. On peut donc appliquer cette fonction au modèle monoroue représenté ci-dessous :
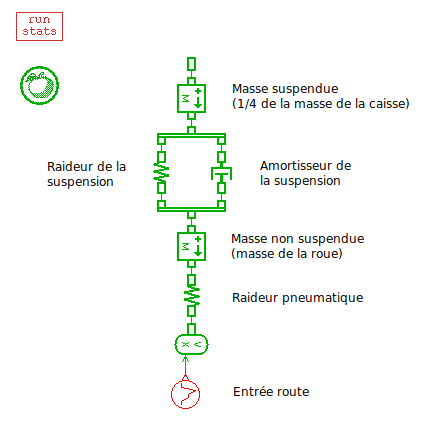
Les perturbations de la route rencontrées lors de la marche du véhicule sont représentées par des sollicitations verticales (de type Signal) en entrée du modèle AMESim.
Dans un premier temps, on s'intéresse au comportement de la suspension au passage d'un trottoir : le véhicule roule et heurte un trottoir ; il s'ensuit une entrée verticale au niveau du sol, de la hauteur du trottoir - on supposera que ce dernier possède une hauteur de 10 cm. Lors du passage du trottoir, la roue et la caisse possèdent les réponses suivantes (le système est à l'équilibre à t = 0) :
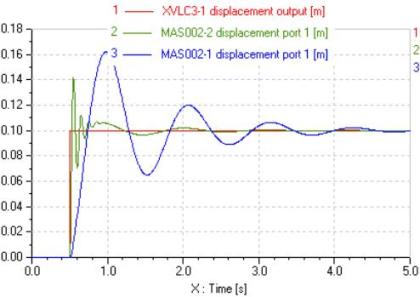
Il apparaît clairement que la caisse et la roue ne possède pas les mêmes réponses à la même sollicitation. Ceci est essentiellement dû à la différence de dynamique qui existe entre ces deux masses. En effet, lorsque les valeurs propres du système sont calculées « numériquement » par AMESim, nous obtenons les valeurs propres suivantes :
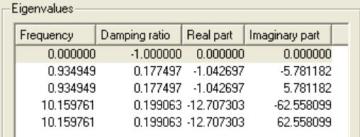
Nous obtenons une dynamique lente à 0.93 Hz et une plus rapide à 10.16 Hz.
Ces deux dynamiques se retrouvent assez clairement sur les graphiques précédent : d'une part sur la réponse de la caisse qui oscille à une fréquence d'environ 1 Hz (soit environ une oscillation par seconde) et d'autre part sur la réponse de la roue, qui oscille à environ 10 Hz (soit une oscillation pour 0,1 s). On peut donc affirmer que la dynamique lente est liée à la caisse et la dynamique rapide à la roue.
Cependant, il convient de vérifier cette première conclusion à l'aide d'une approche analytique, en mettant en équation les mouvements de chacune des masses (roue et caisse). Par cette approche, on devrait pouvoir retrouver des résultats similaires.
Recherche des valeurs propres par une approche analytique
La méthode analytique est appliquée au modèle précédent, qui correspond à un système à deux degrés de liberté. L'étude se fera en deux étapes :
mise en équation du système en exprimant l'équilibre dynamique des deux masses (roue et caisse) ;
passage dans le domaine fréquentiel par transformation de Laplace du système différentiel obtenu.
Équilibre dynamique du système
Équilibre de la roue :
Équilibre de la caisse :
On a vu précédemment que les valeurs propres représentent les dynamiques internes et sont des caractéristiques intrinsèques au système. Elles sont également les racines du dénominateur de toutes les fonctions de transfert que l'on peut calculer sur le système, car n'importe quelle fonction de transfert donnera toujours le même dénominateur. Pour s'en convaincre, on peut calculer les fonctions de transfert du déplacement caisse et du déplacement roue par rapport à l'entrée sol. Pour calculer ces deux fonctions de transfert, il faut passer en Laplace les précédentes équations et éliminer l'effet de la gravité.
Transformation de Laplace
Équilibre de la roue :
Équilibre de la caisse :
Fonctions de transfert
Fonction de transfert déplacement roue / entrée sol :
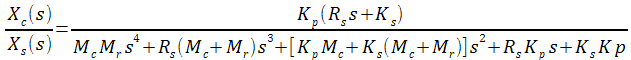
Fonction de transfert déplacement caisse / entrée sol :
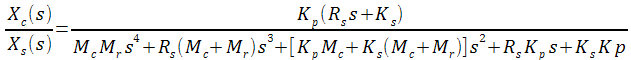
Mise sous forme matricielle
On peut déterminer les valeurs propres du système en exprimant le système différentiel sous forme matricielle. En partant du système ci-dessous,
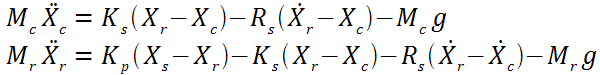
et en considérant que la vitesse est la dérivée d'un déplacement, on obtient les relations suivantes :
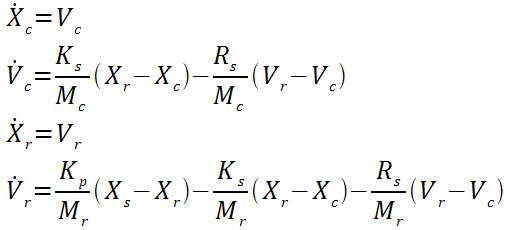
que l'on peut alors exprimer sous forme matricielle :
En appliquant une transformée de Laplace à l'équation matricielle ci-dessus, puis en diagonalisant la matrice obtenue, il est possible de déterminer analytiquement les valeurs propres du système.
Pour la suite, on travaillera avec les résultats numériques obtenus avec AMESim. Cela permet d'obtenir des résultats plus facilement et rapidement que par la méthode analytique.