Vérin symétrique
Jusque là, le modèle de suspension étudié était muni d'un ressort métallique ; mais en réalité, un amortisseur est hydraulique : il est constitué d'un vérin et d'une ou plusieurs restrictions laminant le fluide, créant ainsi de l'amortissement. Il faut donc dimensionner un vérin hydraulique amortisseur possédant un comportement identique à l'amortisseur « mécanique » précédemment étudié. En première approche, on s'intéresse à un vérin symétrique d'une section de 10cm2, ceci afin de faciliter les calculs.
Description du vérin
La figure ci-après montre la représentation schématique d'un vérin symétrique (sous AMESim) :
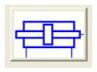
Avec une tige de 5 mm afin de supporter le poids du véhicule, le vérin obtenu possède un corps d'un diamètre de 36 mm.
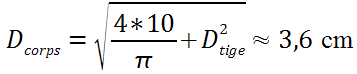
L'amortissement requis est obtenu par laminage du fluide dans une restriction. Connaissant la valeur de l'amortissement (1000 N/(m/s)) et de la vitesse verticale maximale atteinte par une sollicitation du sol (1 m/s), il est possible de déduire les caractéristiques de fonctionnement du vérin :
force maximale : 1000 N appliqués sur une section de 10 cm2 ;
différence de pression maximale : 10 bar ;
débit : 1 dm3/s = 60 L/min.
Ce débit est obtenu pour une différence de pression de 10 bar. L'équation de l'écoulement dans une restriction est donnée par l'équation de Bernoulli :
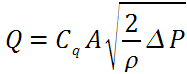
où A est la section de passage (surface totale des restrictions).
Modèle AMESim d'une suspension hydraulique à vérin symétrique
On peut comparer le nouveau modèle de suspension à celui de suspension mécanique étudié précédemment :
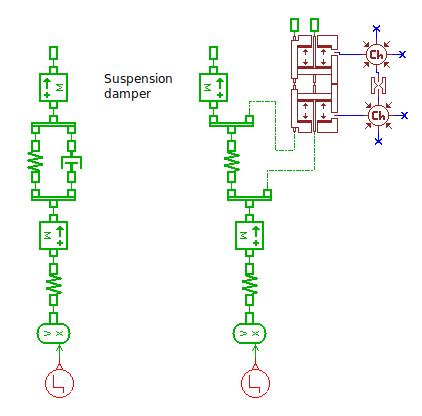
Sans pressurisation du vérin, la pression dans une chambre peut descendre suffisamment bas pour qu'il y ait cavitation. Dans un tel cas, l'amortisseur serait inévitablement détruit au bout d'un certain temps. Il faut donc pressuriser le vérin pour éviter que celui-ci passe en dessous de la pression de vaporisation du liquide utilisé. La différence de pression maximale calculée est de 10 bar ; la pressurisation du vérin doit donc être supérieure à cette valeur de pression. À 25 bar, on obtient la réponse suivante :
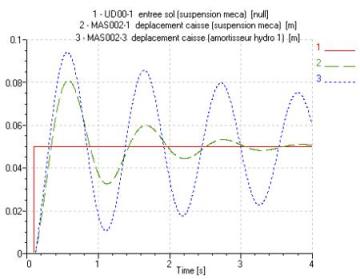
Avec cette configuration, l'amortisseur ne cavite pas car les pressions sont toujours positives.
On observe que le système possédant un amortisseur hydraulique ne donne pas la même réponse que celui muni d'un amortisseur mécanique. Cela est dû à la non linéarité de l'équation de Bernoulli : alors que les couples (60 L/min ; 10 bar), (30 L/min ; 5 bar) et (15 L/min ; 2,5 bar) correspondent à un amortissement identique de 1000 N/(m/s), leurs caractéristiques effort/vitesse sont très différentes de celle de l'amortisseur linéaire.
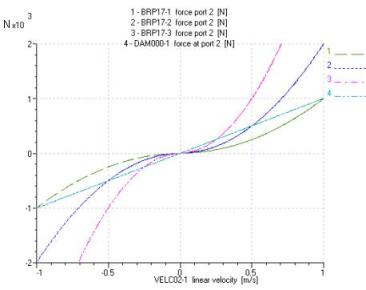
On peut remarquer que la courbe force/vitesse pour un amortisseur de 1000 N/(m/s) passe par les trois points caractéristiques en force et vitesse (250, 0.25), (500, 0.5) et (1000, 1) qui correspondent bien à un amortisseur linéaire de 1000 N/(m/s).
En conséquence, les réponses temporelles pour une sollicitation en entrée sol seront à la fois différentes entre elles et éloignées de celle de l'amortisseur linéaire.
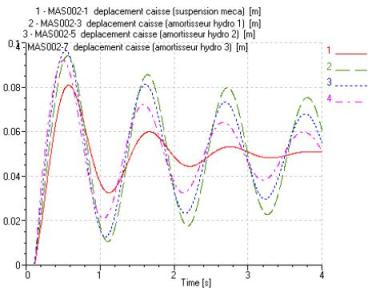
En effet, pour le couple (15 L/min ; 2,5 bar), la courbe temporelle se rapproche le plus de celle théorique de l'amortisseur « mécanique » comme d'ailleurs la courbe de la caractéristique effort/vitesse puisque la vitesse pour une sollicitation de 0.05 m ne dépasse pas les 0.5 m/s en moyenne.
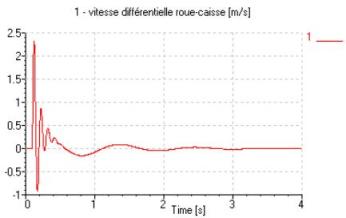
Un amortisseur de voiture est donc un amortisseur non linéaire ; il est alors difficile de déterminer sa réponse fréquentielle (gain et phase).

