Exploitation du modèle avec AMESim
À l'aide des fonctionnalités du logiciel AMESim, il est possible de mener une analyse linéaire du système (mode Linear Analysis) afin de calculer les fonctions de transfert, les valeurs propres et les déformées modales du système. L'exploitation de ces résultats permettra de tirer des conclusions quant au comportement due la suspension.
Fonctions de transfert
Sur les représentations graphiques des fonctions de transfert, le gain est exprimé en décibels (dB). Plus la valeur de ce gain est négative, plus le gain réel se rapproche de zéro et la filtration des perturbations par la suspension augmente.
Gain et phase de la fonction de transfert déplacement roue / entrées sol :
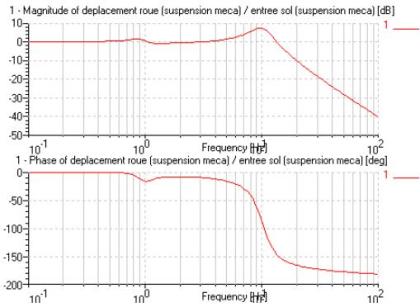
Gain et phase de la fonction de transfert déplacement caisse / entrées sol :
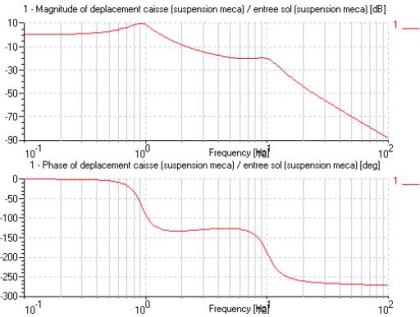
Valeurs propres et déformées modales
Déformées modales en déplacements
Les déformées modales permettent d'obtenir une approximation des valeurs propres, mais également d'identifier les mouvements mis en jeu et donc savoir où positionner un amortisseur pour amortir un mode de vibration particulier. Pour rappel, les valeurs propres ont été déterminées avec AMESim à des fréquences de 0,93 Hz et 10,16 Hz.
La déformée modale du premier mode est obtenue en observant les déplacements des deux masses pour le mode lent de 0,93 Hz.
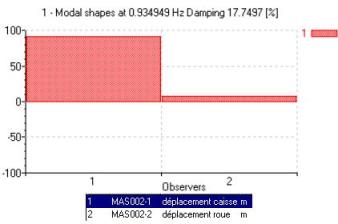
Conformément à une supposition précédente, la contribution de la masse de la caisse est importante par rapport à celle de la roue, pour le mode lent.
Pour le mode plus rapide de 10,16 Hz, la déformée est la suivante :
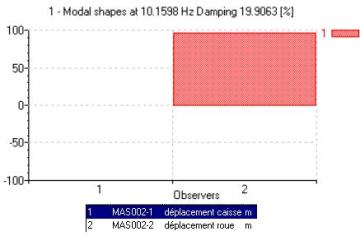
Dans ce cas et comme supposé précédemment, le mode à 10 Hz faire intervenir de manière prépondérante la masse de la roue.
On a ainsi pu déterminer la contribution de chaque masse dans chaque mode.
Déformées modales en efforts
Il est également possible d'afficher les déformées modales non pas en déplacements mais en efforts. Pour cela, on n'étudie plus les déplacements (ou le vitesses) de la roue et de la caisse, mais les efforts dans le ressort de suspension et dans le pneu (qui est modélisé par un ressort). On cherche à savoir quels ressorts contribuent dans chacun des modes propres oscillants, à 0,93 Hz et à 10,16 Hz.
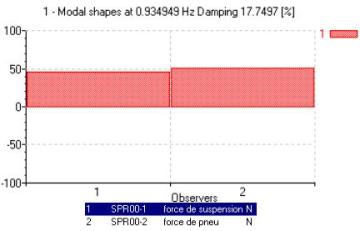
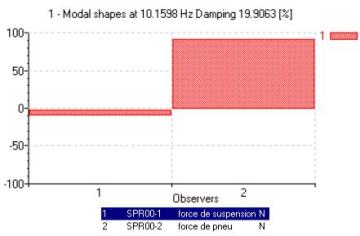
Détermination analytique des modes propres
En analysant les quatres déformées modales obtenues, il est possible de déterminer analytiquement les fréquences des modes propres oscillants et ainsi vérifier la qualité des approximations
Pour le mode lent à 0,93 Hz
La masse de la caisse bouge beaucoup et les deux ressorts se compriment de la même manière. On peut donc en conclure que les deux ressorts travaillent en série (puisque les deux efforts sont identiques) sur le mouvement de la caisse. En conséquence le calcul du mode propre est le suivant (les deux ressorts en série sur la masse de caisse) :
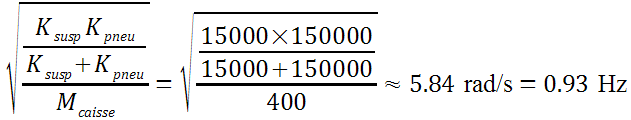
Notre approximation du premier mode est donc bonne.
Pour le mode rapide à 10,16 Hz
Seule la masse de la roue participe. En revanche, les deux ressorts sont en opposition de phase (compression par rapport à détente) et dans des proportions qui correspondent au rapport des raideurs (environ 90% et 10%). Ceci correspond à deux ressorts en parallèle connectés sur la masse de la roue, la masse de caisse à 10 Hz étant considérée comme un bâti fixe. Le calcul du second mode est donc le suivant :
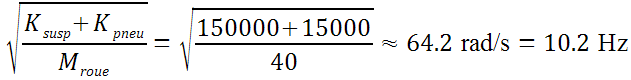
Là encore, l'approximation est excellente.
On constate ici que les déformées modales sont un excellent moyen pour reconstruire analytiquement une approximation des modes propres (ou encore des valeurs propres).
Positionnement de l'amortisseur
Les déformées modales aident également au positionnement de l'amortisseur sur l'ensemble de la suspension lorsqu'une oscillation doit être amortie. Dans un tel cas, l'amortisseur doit être placé entre deux parties dont l'une bouge fortement et l'autre ne bouge pas ou bouge mais dans l'autre sens pour que cet amortisseur soit efficace à la fréquence donnée.
Dans le cas de notre suspension, une localisation de l'amortisseur pourrait être celle montrée ci-après.
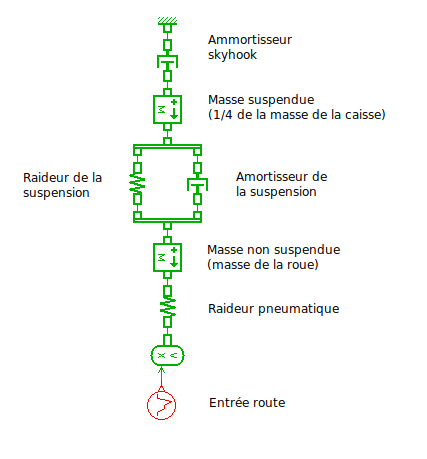
La localisation de l'amortisseur peut paraître étonnante, toutefois ce type d'amortisseur est appelé « Skyhook » (« accroché au ciel »). En fait cet amortisseur relie la caisse au ciel et n'est donc sensé n'amortir que la caisse.

