Modèle de suspension mécanique simplifiée
Visualiser les résultats à partir de l'applet (nécessite que le JRE soit installé dans le navigateur).
Le premier modèle étudié est celui d'un modèle de roue doté d'une suspension simplifiée. L'étude de ce système constitue une base de départ pour l'étude de systèmes plus complexes. Voir le cours »
Établissement du modèle AMESim
Modèle AMESim
Le modèle du système est détaillé ci dessous :
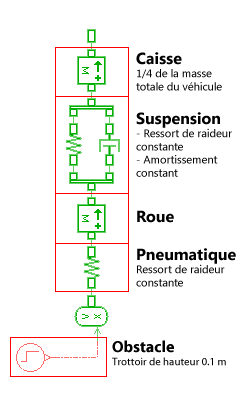
Les valeurs numériques des différents paramètres du système (masses, raideurs, etc.) sont obtenues par recherche bibliographique.
Masse du véhicule/de la caisse
Dans un modèle monoroue, la masse suspendue correspond à un quart de la masse totale du véhicule - en faisant le postulat que le véhicule possède quatre roues et des suspensions identiques.
En ce qui concerne la masse suspendue, il est intéressant de considérer trois types de véhicules, de tailles différentes afin que leurs masses respectives puissent potentiellement avoir une influence sur les résultats : une citadine, une berline et un monospace. Pour chacun d'eux, la valeur du poids maximal autorisé sera utilisée : la suspension du véhicule devrait pouvoir supporter cette condition extrême.
Véhicule | Citadine | Berline | Monospace |
|---|---|---|---|
Masse totale (kg) | 1200 | 2000 | 2800 |
Masse par roue (kg) | 300 | 500 | 700 |
Raideur et amortissement de la suspension
La raideur du ressort K (en N/m) est donnée par la relation :
f est la « fréquence de confort » du véhicule. Elle est faible pour les véhicules de tourisme, en général limitée à 1,5 Hz ; plus élevée pour les véhicules de sport (conférant une conduite plus « ferme » au détriment du confort). Par la suite, on prendra f = 1,0 Hz.
m est la masse suspendue sur une roue, définie dans le paragraphe précédent.
MR est le « Motion Ratio », le rapport du déplacement de la roue par rapport au ressort. Ce paramètre dépend notamment de la géométrie de la suspension. Par la suite, cette valeur sera fixée à MR = 1. Cette valeur peut sembler arbitraire mais l'influence de ce choix sera limitée puisqu'il s'agira principalement d'une étude comparative des résultats obtenus.
L'amortissement A (en N/(m/s)) est quant à lui donné par la relation :
α est le taux d'amortissement. Par la suite, on prendra α = 0,25 ; cette valeur d'amortissement est préconisée pour les véhicules étudiés (véhicules de tourisme) puisqu'elle permet un confort optimal ; elle correspond par ailleurs à un régime d'oscillation pseudo-périodique, ce qui se rapproche de la réalité.
Ainsi, il est possible de déterminer pour chaque véhicule les valeurs - constantes - de la raideur du ressort et de l'amortissement (les valeurs ont été arrondies par souci de simplification, le but étant de donner des ordres de grandeur).
Véhicule | Citadine | Berline | Monospace |
|---|---|---|---|
Raideur ressort K (N/m) | 12000 | 20000 | 28000 |
Amortissement A (N/(m/s)) | 942 | 1570 | 2198 |
Roue et pneumatique
La roue est assimilée à une masse M = 50 kg (environ 10% de la masse suspendue), qui comprend la masse de la roue, de la suspension et d'une partie de l'essieu.
Le pneumatique est assimilé à un ressort simple de forte raideur K = 150000 N/m. Cela correspond à la « souplesse » apportée par la gomme et la chambre à air. Chercher à déterminer de manière exacte cette raideur demanderait une étude de résistance des matériaux (contraintes sur la gomme) et de thermodynamique (compression de l'air présent dans la chambre).
Obstacle
Pour tester la réponse du système, une sollicitation verticale d'une hauteur de 10 cm a été simulée à l'aide d'un signal échelon en entrée. Cette sollicitation modélise le franchissement d'une bordure de trottoir.

