Notions de dimension, d'ordre et de rang des modèles
Définition : dimension d'un modèle Bond Graph
La dimension d'un modèle Bond Graph indique le nombre de variables pouvant potentiellement décrire le comportement dynamique du système. Sur le modèle Bond Graph, la dimension est égale au nombre de variables d'énergie associées aux éléments de stockage d'énergie, augmenté des intégrateurs de la partie signal du modèle. C'est une propriété du modèle acausal (sans causalité).
Exemple : direction assistée électrique
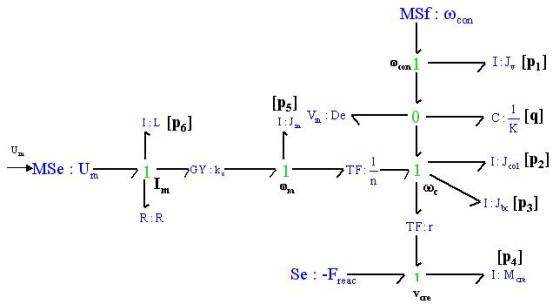
Dans l'exemple ci-dessus, il y a 7 variables d'énergie associées à 7 éléments de stockage et 0 intégrateur dans la partie signal. La dimension de ce Bond Graph est donc :
Définition : ordre d'un modèle Bond Graph
L'ordre d'un modèle Bond Graph indique le nombre de variables statiquement indépendantes qui permettent de décrire le comportement dynamique du système. C'est également le nombre de conditions initiales à fixer. Il est égal au nombre de variables d'énergie associées aux éléments de stockage d'énergie, en causalité intégrale sur le Bond Graph en causalité préférentielle intégrale - BGI, augmenté des intégrateurs de la partie signal du modèle.
Exemple : direction assistée électrique
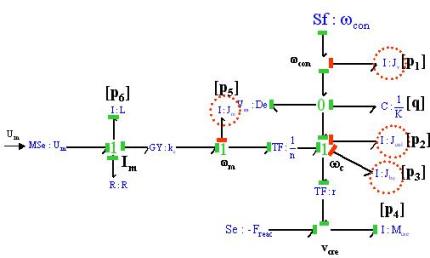
Dans l'exemple ci-dessus, il y a 3 variables d'énergie associées à 3 éléments de stockage en causalité intégrale sur le BGI et 0 intégrateur dans la partie signal. L'ordre de ce Bond Graph est donc :
Définition : rang structurel du système d'équations différentielles
Le rang structurel du système d'équations différentielles issu d'un modèle Bond Graph indique le nombre de variables dynamiquement indépendantes (c'est-à-dire le nombre d'équations indépendantes). Le rang structurel du système d'équations différentielles est égal au nombre de variables d'énergie :
qui sont en causalité intégrale sur le Bond Graph en causalité préférentielle intégrale (BGI) ;
qui passent en causalité dérivée sur le Bond Graph en causalité préférentielle dérivée (BGD) ;
ce nombre est augmenté du nombre d'intégrateurs de la partie signal du modèle.
Remarque : la procédure d'affectation de la causalité préférentielle dérivée est identique à la procédure SCAP, mais dans ce cas les éléments de stockage sont mis de préférence en causalité dérivée.
Exemple : direction assistée électrique
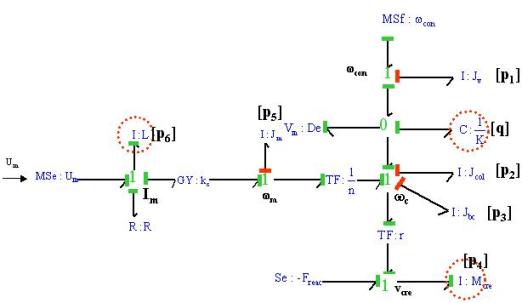
Dans l'exemple ci-dessus, il y a 3 variables d'énergie en causalité intégrale sur le BGI, qui passent toutes en causalité dérivée sur le BGD, et 0 intégrateur dans la partie signal. Le rang structurel du système d'équations différentielles est donc :

