1 : traction uniaxiale élastoplastique
Exercice 1 : traction élastoplastique
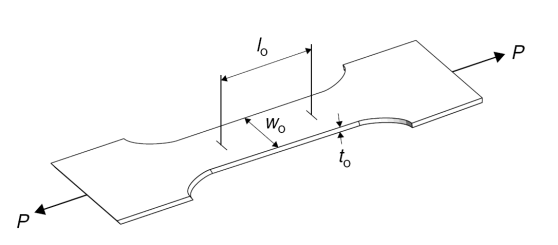
On considère une éprouvette de traction uni-axiale dont la longueur utile initiale L0 = 50mm , la largeur w0 = 12.5mm et l'épaisseur t0= 0.8mm. La charge initiale est Fint=1.791kN et on mesure la charge au point quelconque A tel que FA = 2,059 kN et l'extension correspondante UA= 1,22mm. La charge maximale Fmax=2,94kN et cela se produit à une extension U= 13,55mm. L'éprouvette est rompue à une extension Umax= 22,69mm. Déterminer :
1. Section initiale de l'éprouvette.
2. Contrainte initiale.
3. Contrainte et déformation varies maximales.
4. Contrainte et déformation vraies au point A.
5. En adaptant une loi de puissance σ = K . εn à deux points, le point A et le point de charge maximum, déterminer le coefficient d'écrouissage n et la valeur de K.
Solution :
1. Section initiale de l'éprouvette : S0= w0 . t0 = 0.8 x 12.5 = 10 mm2
2. Contrainte initiale : σinit= Fint/S0= 1791/10=179.1 N/mm2
3. Contrainte et déformation varies maximales : σvraie= Fmax/S
Calcul de la section S avec conservation de la masse donc le volume : V = V0 → S . L = S0 . L0 → S = S0 . L0/L → S = S0 . L0 / (L0 + U)
On pose déformation ingénieur : ε = ( L - L0 )/L0 = U/L0 =13.55 / 50 = 0.721
La section courante : S = S0 /(1 + ε ) = 10 /(1+0.721) =7.86 mm2
Contrainte vraie : σvraie= Fmax/S =2940/7.86=373.6 N/mm2
Déformation vraie : εvraie= Ln(L/L0)=Ln((L0+ U)/L0)=Ln(1+ε)=Ln(1+0.721)=0.54
4. Contrainte et déformation vraies au point A :
Déformation ingénieur au point A : εA = UA/L0 =1.22 / 50 = 0.0244
La section courante : SA = S0 /(1 + εA ) = 10 /(1+0.0244) =9.76 mm2
Contrainte vraie : σvraie= FA/SA = 2059/9.76 =211 N/mm2
Déformation vraie : εvraie=Ln(1+εA)=Ln(1+0.0244)=0.024
5. En adaptant une loi de puissance σ = K . εn à deux points, le point A et le point de charge maximum, déterminer le coefficient d'écrouissage n et la valeur de K.