6 - Le remaillage pour la simulation numérique
Pourquoi la simulation numérique?
Dans les contextes actuels de développement industriel, les outils de simulation virtuelle sont devenus indispensables à la gestion des compromis et à la bonne prévision des performances.
Dans le monde virtuel du modèle, le concepteur doit définir les hypothèses et maîtriser les risques associés.
Durant la phase de conception d'un dispositif ou d'un système quelconque, le concepteur doit proposer une configuration satisfaisante au mieux les besoins fonctionnels, et en même temps, viable d'un point de vue économique.
La recherche de la meilleure performance d'un dispositif dans laquelle interviennent des paramètres techniques, structurels, dimensionnels et physiques est un problème difficile.
Cette recherche croissante de maîtrise entraîne une augmentation de la complexité des modèles et une augmentation des cas à étudier
La simulation numérique : Une démarche interdisciplinaire
La complexité des phénomènes qui apparaissent seuls ou conjugués nécessite l'utilisation de procédures de calcul puissantes combinant simulation numérique et outil d'optimisation
L'optimisation multidisciplinaire sert à optimiser la conception ou le processus de pilotage de systèmes complexes qui nécessitent l'utilisation de simulateurs ou d'essais réels pour mesurer leurs performances.
Ces simulateurs peuvent être de nature différente : des simulations numériques traitements des phénomènes physiques ou des simulations événementielles (traitements d'événements).
La complexité des phénomènes qui apparaissent seuls ou conjugués nécessite l'utilisation de procédures plus puissantes combinant simulation numérique et outil d'optimisation.
Les outils apportés permettront de remplacer les modélisations souvent lourdes et complexes par des équations mathématiques simples et suffisamment prédictives en vue de réduire les temps de calcul et gagner en réactivité.
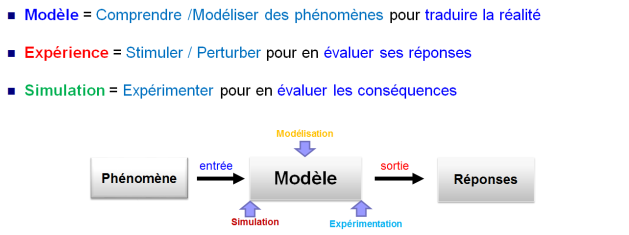
La simulation numérique : Une démarche interdisciplinaire
Les calculs de simulation permettent de prédire le comportement du sujet étudié sans avoir à passer par la construction de prototypes ou la réalisation d'essais réels, coûteux et/ou difficiles à mettre en place ; ce qui est un avantage essentiel en matière de coûts de production, notamment dans les domaines innovants.
Cependant, une simulation numérique est bien souvent coûteuse en terme de temps de calcul (une heure, une nuit, ..., une semaine).
L'application des méthodes d'optimisation nécessite de nombreuses simulations numériques (au mieux, des dizaines lorsqu'il est possible d'utiliser un algorithme d'optimisation déterministe performant, au pire, des milliers lorsque la recherche d'un optimum global est effectuée grâce à un algorithme évolutionniste et peut donc induire un coût global des simulations prohibitif qui la met hors de portée d'un usage courant.
Elles peuvent aussi, dans une optique d'optimisation, aboutir à des économies rationnelles de matériaux, à une amélioration de la qualité ou de la durée de vie des produits et/ou à une optimisation des processes de production.

La simulation numérique : Une démarche interdisciplinaire
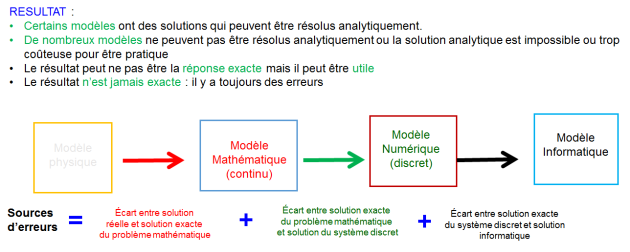
Modélisation Mathématique
Formulation du modèle physique multidisciplinaire
Existence/unicité si c'est possible des solutions, problème bien pose
Propriétés qualitatives des solutions (régularité, homogénéité, stabilité)
Modélisation Numérique
Conception des modèles en s'appuyant sur les bases physiques
Fiabilité et convergence des modèles
Estimation d'erreurs des modèles et méthode numériques
Modélisation Informatique
Algorithme : rapidité, efficacité et convergence
Exécution : automatique ou intelligente
Efficacité : réduire les coûts de calcul aussi petit que possible
Rapidité : optimisation et parallélisme
La simulation numérique : Une démarche interdisciplinaire
Un résultat de simulation sans estimation de l'erreur ne sert a rien! Plusieurs sources d'erreur :
mise en équation des phénomènes physiques
données du problème (paramètres, conditions initiales, conditions extérieurs et aux limites)
approximation par une méthode numérique
erreurs d'arrondi, erreurs humaines, tolérances des convergences
précision machine et programmation
Question : qu'est-ce qu'un Bon Modélisateur ? → Estimer et Contrôler les Erreurs
Objectifs d'une simulation :
Convergence : erreur arbitrairement petite en y mettant les moyens
Fiabilité : garantir que l'erreur soit en dessous d'une certaine tolérance
Efficacité : coût de calcul aussi petit que possible

Qu'est-ce que la Simulation Numérique ?
Une équation différentielle est une équation mathématique qui relie une fonction à ses dérivés partielles d'une ou plusieurs variables dépendantes avec une ou plusieurs variables indépendantes,
Dans les applications, les fonctions représentent généralement des quantités physiques, les dérivés représentent leurs taux de changement, et l'équation définit une relation entre les deux.
De nombreux comportements physiques sont régis par des équations aux dérivées partielles (EDP)
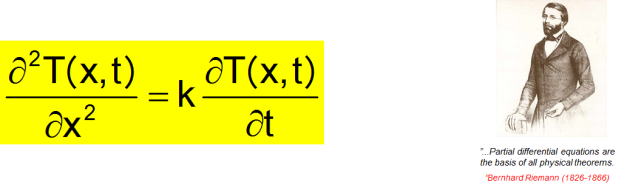

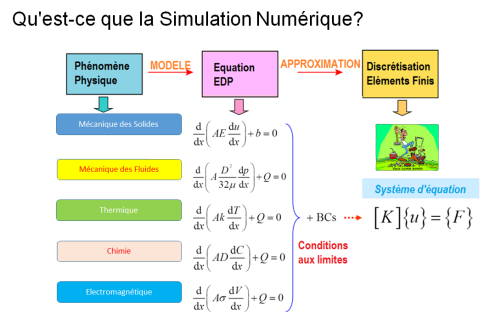


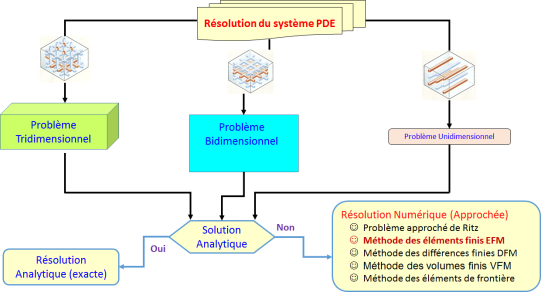
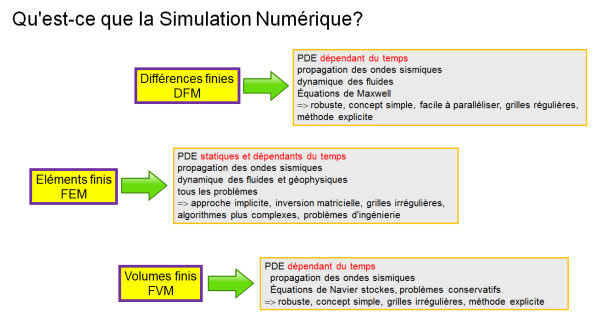
Qu'est-ce que la Simulation Numérique par éléments-finis ?
La méthode des éléments finis est une méthode de résolution approchée d'équations aux dérives partielles EDP
Elle consiste à remplacer un Problème Compliqué pour lequel a priori on ne connaît pas de solution, par un problème Plus Simple que l'on sait résoudre
L'objectif de la méthode des éléments finis est de déterminer des fonctions inconnues telles que les fonctions déplacements, contraintes, température, pression, vitesse, champ électrique dépendant ou non du temps et de l'espace
La méthode des éléments finis englobe trois domaines principaux.
Les méthodes de discrétisation permettent de transformer un problème continu en une approximation discrète
Les méthodes variationnelles permettent de transformer EDP en une forme approchée variationnelle
Les méthodes numériques qui permettent de résoudre les systèmes d'équations
Résolution par la Méthode des Éléments Finis d'un problème physique formulé en termes d'Equations aux Déviées Partielles s'appuie sur :
Discrétisation spatiale (maillage) du domaine
Discrétisation temporelle
Génération de maillages : un verrou scientifique
Géométries complexes ?
Procédures automatiques ?
Qualité géométrique des éléments ?
Impact sur la précision ?
Erreurs de discrétisation ?
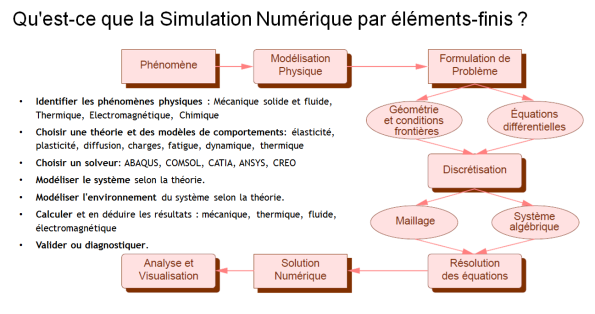
Le maillage en Simulation Numérique
Il existe 6 sources d'erreurs dans la solution :
Erreur due aux hypothèses du modèle
Erreur due aux traitements numériques (arrondi, intégration numérique, ...)
Erreur due aux non respect de la géométrie
Erreur aux dégrées d'approximation
Erreur due aux approximations des conditions aux limites
Erreur due aux approximations des charges appliquées (mécanique, pression, vitesse, température, courant électrique, champ magnétique, ,,,)
Le maillage des éléments est l'étape la plus longue et délicate de la chaîne de calcul. La qualité du maillage est déterminante dans la précision, convergence et qualité de l'analyse. L'optimisation du maillage : mettre le nombre qu'il faut d'éléments là où il faut
Pour les modèles courants de l'industrie (géométrie complexe): impossible de créer un maillage composé d'éléments tétraédriques, hexaédriques ou quadrangulaires ou triangulaires parfaits
Certains éléments générés peuvent avoir des arêtes plus longues que d'autres:
Petites arêtes
Géométries courbes
Fonctions minces et d'angles vifs
Il faut définir de critères sur les qualités des maillages
Les qualités d'un mailleur sont principalement :
• Robustesse : quelle que soit la géométrie proposée, il doit être capable de construire, si possible automatiquement, un maillage correspondant ;
• Précision : le maillage doit coller le plus possible au contour de la géométrie, de façon à avoir le minimum de perte de volume ;
• Régularité : la qualité des éléments du maillage doit être bonne et suffisamment régulière, afin de minimiser l'approximation réalisée par la méthode des éléments finis ;
• Souplesse : on doit pouvoir mailler plus finement certaines zones de la pièce où les phénomènes que l'on désire étudier sont plus fins ;
• Rapidité : créer un maillage qui prend encore plus de poids lorsque l'on désire développer un remailleur automatique
• Capacité à évoluer : il doit être suffisamment modulable pour pouvoir générer de nouveaux types d'éléments, ou lui imposer une structure particulière.
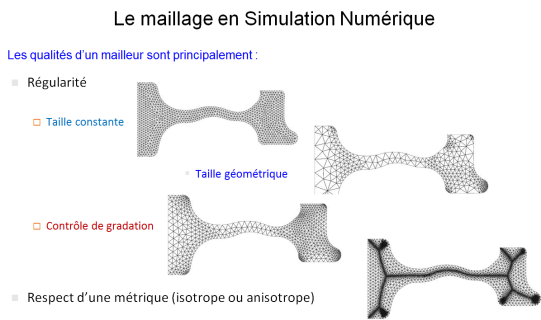
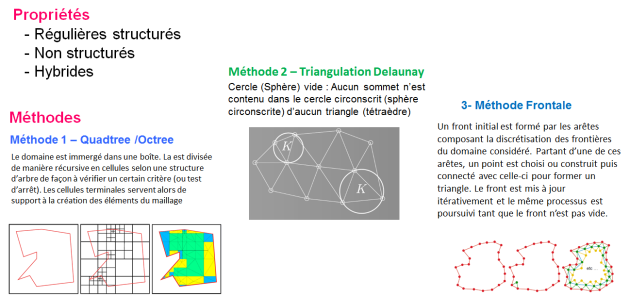
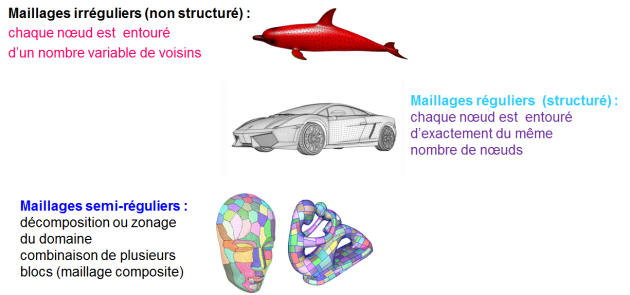
Maillage structuré : Avantages
• Bon contrôle de la qualité (précision et orthogonalité des mailles aux parois)
• Utilisable par codes de calculs rapides
• Description légère (Connectivité simple)
• Modifications aisées, maillage paramétrique (géométrie variable)
• Automatisation partielle de la création de la topologie
Maillage non-structuré : Avantages
• Plus automatique (pas de création de topologie)
• Très bien adapté aux formes complexes
• Dopé par l'adaptation ou le maillage hybride (par exemple tétraèdres/prismes) pour une utilisation croissante
Maillage structuré : Inconvénients
Mise en œuvre difficile et longue pour les formes complexes
Expertise humaine requise : création d'une topologie
Difficile d'obtenir une bonne qualité de maillage pour certaines géométries complexes
Maillage non-structuré : Inconvénients
Contrôle local du maillage moins aisé
Description des éléments lourde (informatique)
Demande plus de temps CPU, de mémoire vive et très gourmand en nombre de mailles
Connectivité complexe
Génération moins robuste que la génération de maillages structurés
Engendre des erreurs numériques
Maîtrise de l'erreur du calcul éléments finis
Les questions essentielles auxquelles l'ingénieur devra répondre s'il veut effectuer une analyse par un modèle numérique dans de bonnes conditions, sont :
Quel modèle mathématique utiliser ?
Quel modèle numérique faut-il lui associer ?
Quelle est l'erreur d'approximation commise ?
Peut-on améliorer le modèle numérique ?
Faut-il changer le modèle mathématique ?
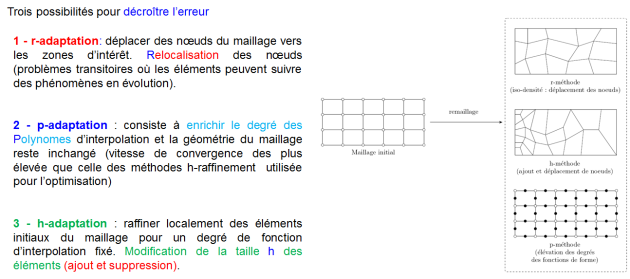


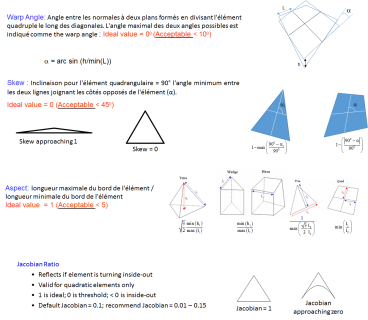
Le remaillage en Simulation Numérique
Une des méthodes les plus simples pour garantir une bonne qualité des éléments et optimiser un maillage est de :
Partir d'un maillage plus ou moins grossier
Raffiner uniformément jusqu'à la stabilisation des champs mécaniques.
Le choix du maillage compromis entre :
Coût de calcul
Niveau de précision
Une solution avec une précision connue à moindre coût → Un estimateur d'erreur physique et géométrique couplé avec une méthode de remaillage adaptatif → Procédure d'adaptation du maillage automatique
Il existe différents critères de déclenchement du remaillage :
mesure du taux de pénétration du maillage à l'intérieur des outils
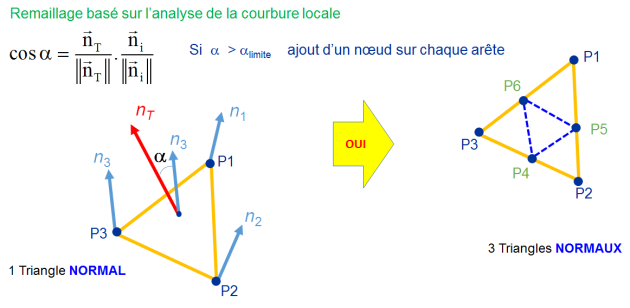
mesure de la courbure des côtés frontières
dégénérescence des éléments (jacobien de la transformation sur l'élément de référence négatif ou nul)
interpénétration de la matière (défaut de repli)
Procédure d'adaptation du maillage automatique :
1. Effectuer un premier calcul avec un maillage initial grossier
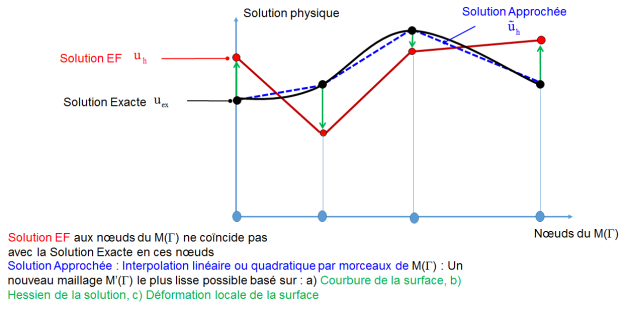
2. Évaluer les erreurs de discrétisation
3. Déterminer la nouvelle carte de taille d'éléments permettant d'obtenir une précision donnée tout en minimisant les coûts de calcul
4. Construire la nouvelle discrétisation spatiale du maillage
5. Calculer le pourcentage d'idéalité du maillage (qualité)
6. Si le pourcentage d'idéalité est inférieur au seuil demandé, une nouvelle itération doit être effectuée
7. Transfert des champs physiques
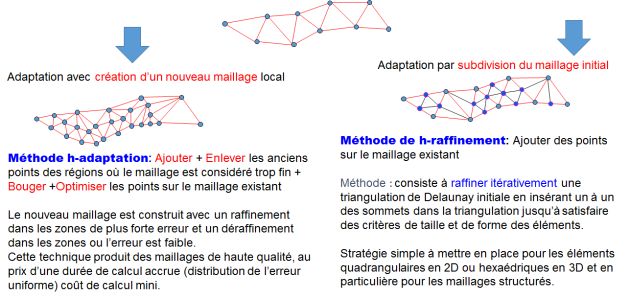




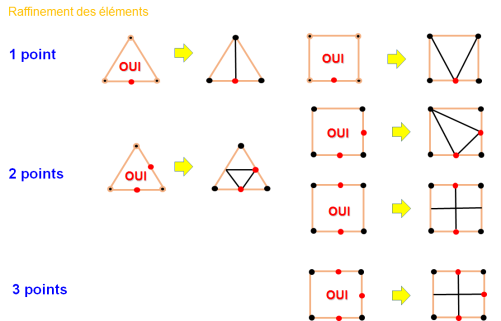
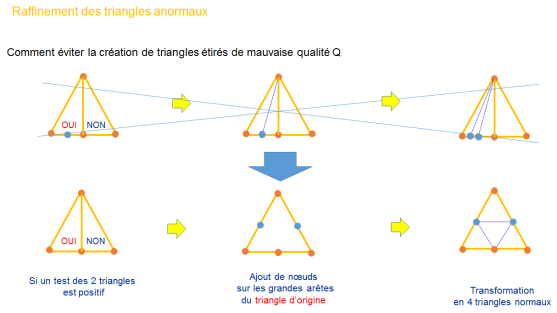
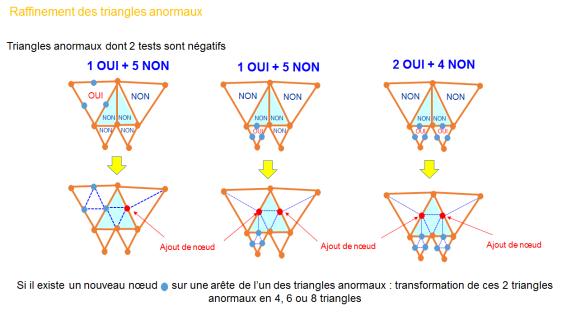
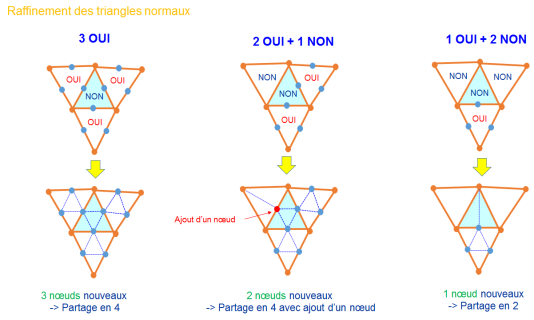
Le remaillage avec le logiciel Forge :
Le remailleur automatique 2D de FORGE2® permet de générer automatiquement des maillages triangulaires en 7 étapes :
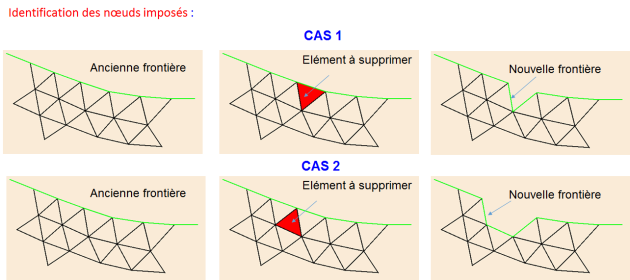
sur discrétisation de la frontière de l'ancien maillage par ajoute des points supplémentaires aux nœuds frontaliers de l'ancien maillage.
optimisation de la frontière par suppression de la description de la frontière certains points de sur discrétisation. La frontière décrite par les points restants doit vérifier un certain nombre de critères : précision, courbure maximale et homogénéité entre les segments successifs.
triangulation du nuage de points frontière ainsi obtenu par un algorithme de Delaunay.
reconnaissance de la frontière et suppression des triangles extérieurs au domaine à mailler.
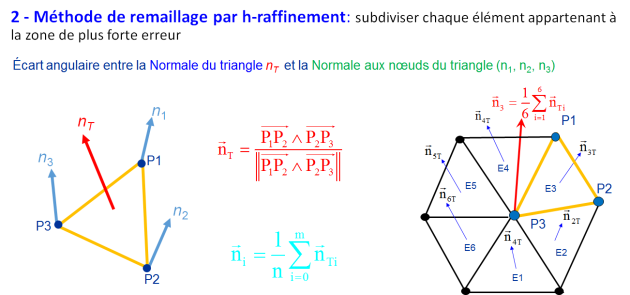
ajout des nœuds internes : on réalise une première ébauche de maillage par une triangulation à l'aide d'éléments à 3 nœuds.
régularisation et amélioration topologique par inversion des diagonales.
ajout des nœuds au milieu de chaque arête, pour former des éléments triangulaires quadratiques.