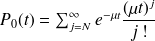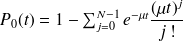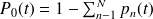Processus de naissance et de mort
A un instant t, l'état d'un système de files d'attente, noté n(t) est le nombre de clients présents dans le système. L'ensemble des variables aléatoires décrit un processus stochastique {n(t) : t>=0}. On considère alors un système dans lequel on ne prend en compte que les processus d'arrivée et de sortie sans tenir compte du nombre de serveurs par exemple. On peut alors introduire la définition suivante :
Définition : Processus d'état stochastique
Le processus d'état stochastique {n(t): t>=0} est un processus de naissance et de mort si pour chaque n=0,1,..., il existe des paramètres
 (avec
(avec
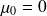 ) tels que, lorsque le système est dans l'état n, le processus d'arrivée est poissonnien de taux
) tels que, lorsque le système est dans l'état n, le processus d'arrivée est poissonnien de taux
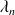 et le processus de sortie est poissonnien de taux
et le processus de sortie est poissonnien de taux
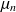 .
.
Définition : Processus de naissance pur
Dans un processus de naissance pur,
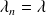 et
et
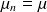 pour n=0,1,... Donc les arrivées ont lieu à taux constant et il n' y a aucun départ. De plus, le nombre de clients dans le système est égal au nombre d'arrivées enregistrées pour un processus de Poisson classique, on a donc :
pour n=0,1,... Donc les arrivées ont lieu à taux constant et il n' y a aucun départ. De plus, le nombre de clients dans le système est égal au nombre d'arrivées enregistrées pour un processus de Poisson classique, on a donc :
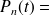 probabilité que l'état du système à l'époque t soit égal à n
probabilité que l'état du système à l'époque t soit égal à n
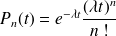
Définition : Processus de mort pur
Dans un processus de mort pur, l'ensemble des états du système est {0,1,...,N} et
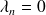 pour n=0,1,...,N
pour n=0,1,...,N
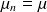 si
si
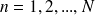 et
et
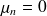 si
si
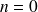
L'état d'un tel système vaut N, il n'y a pas d'arrivée et les départs se produisent à taux constant jusqu'à ce que le système soit vide. On a donc les résultats suivants :
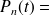 probabilité que N-n départs se produisent dans l'intervalle [0,t]
probabilité que N-n départs se produisent dans l'intervalle [0,t]
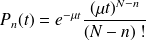
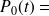 probabilitéque N départs au moins se produisent dans l'intervalle [0,t]
probabilitéque N départs au moins se produisent dans l'intervalle [0,t]