Exemples de systèmes
M/M/1
Un système M/M/1 définit un processus de naissance et de mort caractérisé par les paramètres d'arrivée
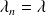 = pour n=0,1,..., et les paramètres de sortie
= pour n=0,1,..., et les paramètres de sortie
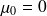 et
et
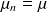 pour n=1,2,...
pour n=1,2,...
Si nous sommes dans les conditions de la loi de Little, nous pouvons donc exposer un certains nombre de définitions.
La quantité
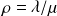 est appelée intensité du trafic. Si les probabilités stationnaires existent, alors elles doivent satisfaire à la formule suivante :
est appelée intensité du trafic. Si les probabilités stationnaires existent, alors elles doivent satisfaire à la formule suivante :
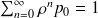
On sait que, si
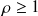 , alors la série diverge, et donc l'équation précédente n'a pas de solution. Par contre, si
, alors la série diverge, et donc l'équation précédente n'a pas de solution. Par contre, si
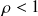 , alors la série converge et les probabilités stationnaires sont définie par les relations suivantes :
, alors la série converge et les probabilités stationnaires sont définie par les relations suivantes :
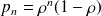
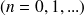
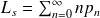
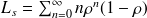
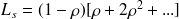
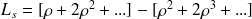
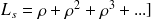
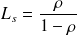
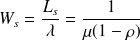
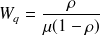
Et finalement on obtient la formule suivante pour la loi de Little :
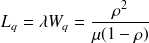
M/M/c
On obtient une description du système en posant
 pour n=0,1,...., et
pour n=0,1,...., et
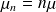 si
si
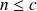 et
et
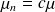 si
si
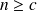
Lorsque le nombre de clients présents dans le système est inférieur au nombre de serveurs, alors les n serveurs occupés donnent lieu à un processus de départ poissonien de taux
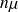 . Si le nombre de clients présents excède c, alors le taux du processus de départ reste limité à
. Si le nombre de clients présents excède c, alors le taux du processus de départ reste limité à
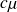 .
.
De même on obtient les formules suivantes :
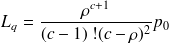
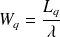
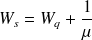
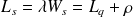
Tous ces résultats seront utilisés dans l'exemple développé avec ce cours en ligne.





