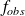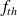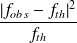Correction partie 2
Question 1
On souhaite calculer l'espérance de cette distribution, qui est définie par :
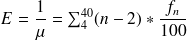. On note que
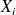représente les effectifs présents dans les données.
On obtient alors :
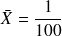(2x34+6x22+10x14+14x10+18x7+22x4+26x3+30x3+34x2+38x1)
9,68.
Question 2
A ce niveau, on peut supposer que la loi de distribution observée précédemment se rapproche d'une loi théorique classique : La loi Exponentielle ( loi des services). Pour le vérifier, on va utiliser le test
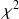de Pearson.
L'espérance d'une loi Exponentielle est égale à l'inverse de son paramètre
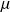. On a donc ici
.
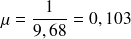Il nous faut calculer les fréquences théoriques d'une loi Exponentielle de paramètre
.
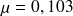On a :
.
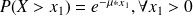et donc
.
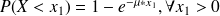On s'intéresse ici à des intervalles. On utilisera donc la technique suivante :
Utilisation de la seconde définition de la probabilité pour le premier terme du tableau.
Du deuxième jusqu'à l'avant dernier :
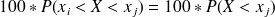- Effectif jusqu'à
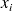.Pour le dernier intervalle : 100 - Somme des Effectifs des intervalles précédents.
Durée | Fréquences observées
| Fréquences théoriques
|
|
<4 | 34 | 33,8 | 0,0007 |
4 à 8 | 33 | 22,4 | 0,007 |
8 à 12 | 14 | 14,8 | 0,045 |
12 à 16 | 1 | 9,8 | 0,004 |
16 à 20 | 7 | 6,5 | 0,041 |
20 à 24 | 4 | 4,3 | 0,019 |
24 à 28 | 3 | 2,8 | 0,009 |
28 à 32 | 3 | 1,9 | 0,67 |
32 à 36 | 2 | 1,2 | 0,46 |
36 à 38 | 1 | 0,8 | 0,04 |
>38 | 0 | 1,6 | 1,6 |
On obtient une valeur de notre statistique de test égale à 2,9.
Afin de déterminer la région critique, il faut se référer à la table du
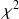. On a un système à 9 degrés de liberté (11 classes - 1 - 1 paramètre dans la loi de Poisson).
De plus, on veut un test avec un risque de 5%. Dans les tables, on lit la valeur 3,33. On a donc une région critique de la forme : R={Z>3,33}.
On accepte donc l'hypothèse d'une distribution exponentielle.
