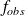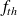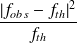Problème files d'attente

On souhaite calculer l'espérance de cette distribution, qui est définie par : 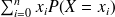. On note que 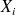représente les effectifs présents dans les données.

La valeur de chaque 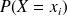est la fréquence observée divisée par le nombre d'observations.

On obtient alors : 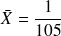(5x0+12x1+22x2+23x3+18x4+13x5+6x6+4x7+1x8+1x9+0x10) 3,267.

On souhaite modéliser notre distribution par une loi de Poisson de paramètre 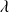t . La densité de cette loi est définie par :

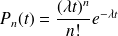
Or, l'espérance d'une loi de Poisson est égale à son paramètre. De plus, on vient de calculer l'espérance de notre distribution, on a donc : 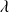t = 3,267.

Nous devons maintenant procéder à un test statistique afin de confirmer, avec un certain risque, que ce modèle est bien représentatif de la distribution que nous avons. Nous allons donc effectuer un test du .

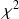On va donc calculer les différentes valeurs du tableau fourni. Dans un souci de clarté, nous allons normaliser tous les effectifs à 100. On a donc : 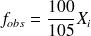, pour i allant de 0 à 10.

Pour les fréquences théoriques, il s'agit de calculer la valeur de : 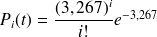pour i allant de 0 à 7 et i=9. Ensuite, nous multiplions cette valeur par 100 afin de tout normaliser.

Tableau pour le test du

N	Fréquences observées	Fréquences théoriques
0	4,762	4,243	0,064
1	11,429	13,407	0,292
2	20,952	21,182	0,002
3	21,905	22,312	0,007
4	17,143	17,627	0,013
5	12,381	11,140	0,138
6	5,714	5,867	0,004
7	3,810	2,649	0,509
>7	1,905	1,530	0,09

On obtient une valeur de notre statistique de test égale à 1,122.

Afin de déterminer la région critique, il faut se référer à la table du 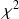. On a un système à 6 degrés de liberté (8 classes - 1 - 1 paramètre dans la loi de Poisson).

De plus, on veut un test avec un risque de 5%. Dans les tables, on lit la valeur 1,64. On a donc une région critique de la forme : R={Z>1,64}.

On a 1,122<1,64 donc on accepte le fait que le modèle poissonnien représente la distribution qu'on a, avec un risque de 5% (pour la moyenne qu'on a trouvé en question 1).

: pour un test de niveau 1%, on a une valeur tabulée égale à 0,372, et alors on se trouve dans notre zone de rejet ! Donc on n'accpeterais pas notre modèle pour représenter nos données, avec un risque de 1%.