Correction Question 3
Le nouveau projet du garagiste donnerait une file d'attente du type M/M/2/4.
On peut analyser le problème directement en recherchant les équations d'état du régime permanent.
Les états sont à nouveau distingués par le nombre de voitures se trouvant dans le système et il y a 5 états puisqu'il y a quatre places (deux sur les ponts et deux dans la file d'attente), plus l'état vide.
On écrit les équations d'équilibre du régime permanent comme au b), mais cette fois, le taux de service est multiplié par 2 lorsqu'il y a au moins deux voitures dans l'état de départ (ou ce qui revient au même, la probabilité d'avoir une fin de service est multipliée par 2 sur l'intervalle Δt), on obtient alors:
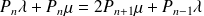
d'où
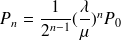
En utilisant le fait que la somme des probabilités vaut 1, on a:
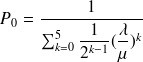
d'où on obtient avec
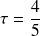 ,
,
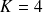 et
et
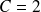 :
:
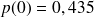
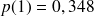
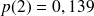
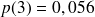
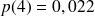
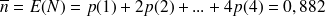
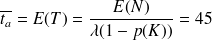 mn
mn
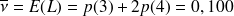
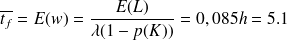 mn
mn
Il reste à calculer le nouveau bénéfice journalier du garagiste. Pour cela, on cherche le nombre de clients servis, il y en a aucun avec la probabilité Po, un seul avec la probabilité P1 et deux avec la probabilité P2 + P3 + P4 = 0,139 + 0,056 + 0,022 = 0,217.
La somme des durées d'occupation des ponts est donc de:
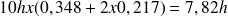
Le nombre moyen de voitures traitées par les deux ponts est donc de
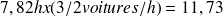
Le nombre moyen de voitures refusées par jour est donc de
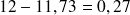
Quand au bénéfice du garagiste, il est par jour de 11,73 x 50 € = 586,50 €
soit un gain journalier par rapport à la solution 2 de 586,50-546,70 = 39,80 €
en supposant que le garagiste travaille 300 jours par an sur les 5 années considérées, cela fait 1500 jours et donc un gain de 59 700 € qui ne couvre pas les 80 000 € d'investissement nécessaires à la construction du deuxième pont.
Cette proposition n'est donc pas intéressante pour le garagiste.





