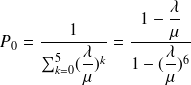Correction Question 2
L'arrêté préfectoral rend la file d'attente du type M/M/1/5
On peut alors soit analyser le problème directement en recherchant les équations d'état du régime permanent (voir la correction en fin de partie b)), soit plus simplement utiliser les formules.
On peut calculer les probabilités d'avoir 0, 1, 2, 3, 4 ou 5 voitures dans le garage:
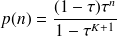
d'où on obtient avec
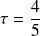et
:
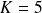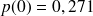
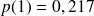
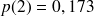
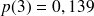
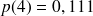
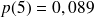
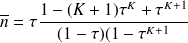
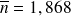
(on aurait obtenu le même résultat en calculant
)
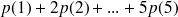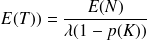soit pour l'application numérique
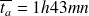
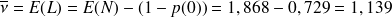
(on aurait obtenu le même résultat en calculant
)
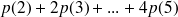soit pour l'application numérique
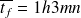
Il reste à calculer la nouvelle valeur du bénéfice journalier du garagiste. Pour cela, il faut calculer combien de voitures sont traitées en moyenne par jour.
On peut l'obtenir de deux façons différentes.
Ou bien on calcule
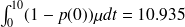voitures
(formule que l'on peut aussi obtenir en constatant que
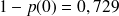donne la probabilité qu'il y ait une voiture dans le système et donc que le pont élévateur soit en activité ; le pont fonctionne donc en moyenne seulement 7,29 h par jour, ce qui lui permet de traiter
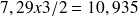voitures par jour en moyenne).
Ou bien on calcule
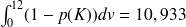voitures
(formule que l'on peut encore obtenir en considérant qu'il arrive en moyenne 12 voitures par jour et que la probabilité qu'une voiture reste dans le système est de 1-P(K)).
On obtient donc un bénéfice moyen de 50€ x 10,934 = 546,70€ d'où un préjudice dû à l'arrêté préfectoral de
600 € - 546,70 € = 53,30 € et 12-10,934=1,066 clients en moyenne refusés chaque jour.
Nous rappelons enfin brièvement comment on peut obtenir la formule donnant la valeur des p(n):
Le système comporte 6 états distincts de E(0) à E(5).
En régime permanent, on a pour n≠0 et n≠5 (où certains termes n'existent pas):
P(E(n)∅E(n+1))+P(E(n)∅E(n-1))=P(E(n+1)∅E(n))+P(E(n-1)∅E(n))
soit en raisonnant sur un intervalle Δt:
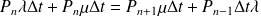
En simplifiant par Δt, on obtient:
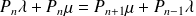
d'où
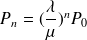et en utilisant le fait que la somme des probabilités vaut 1, on a:
