Correction Question 1
Nous avons bien un problème de file d'attente où le service est constitué des travaux réalisés sur le pont élévateur et où les clients sont les voitures.
Si nous voulons appliquer les résultats du polycopié ou des transparents de cours, il serait mieux que la file soit, selon les notations de Kendall, du type M/M/1, c'est-à-dire arrivées poissonniennes (ou loi inter-arrivées exponentielle), service exponentielle et un seul serveur.
En ce qui concerne la durée du service, l'énoncé ne fournit qu'un seul renseignement: la durée moyenne d'un service est égale à 40 mn (soit 2/3 d'heure). Donc, en moyenne, dans une journée de 10h, on peut traiter 10x3/2=15 voitures.
En absence de tout autre indication, on admettra que la durée du service suit une loi exponentielle de moyenne 2/3 (μ=3/2, nombre moyen de services par unité de temps), puisque c'est la loi la plus fréquente.
quel est le type de la loi d'arrivée des clients, ainsi que ses paramètres ?
En ce qui concerne la loi des arrivées, nous avons des statistiques pour les arrivées journalières sur 100 jours (=7+24+48+20+1).
Nous pouvons en déduire:
la moyenne des arrivées journalières:
m=12.1
Elle est proche de 12 voitures par jour.
Si nous supposons que les arrivées de voitures suivent une loi poissonnienne de moyenne journalière de 12, alors la probabilité d'avoir n arrivées un jour donné est définie par :
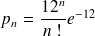
Les valeurs des
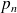ont été fournies en annexe avec l'énoncé.
Pour vérifier l'hypothèse selon laquelle les valeurs fournies suivent bien une loi de poisson de moyenne 12, on va effectuer un test du χ2. On commence par comparer, pour chaque tranche de valeurs, la valeur théorique avec la valeur expérimentale, les résultats sont résumés dans le tableau suivant:
Ordre de grandeur de la demande journalière | Probabilité théorique selon la loi de Poisson de moyenne 12 | Nombre théorique d'apparition de cette demande | Nombre expérimental d'apparition de cette demande |
moins de 5 | 0.021 | 2.1 | 7 |
6 à 10 | 0.327 | 32.7 | 24 |
11 à 15 | 0.497 | 49.7 | 48 |
16 à 20 | 0.144 | 14.4 | 20 |
21 à 25 | 0.011 | 1.1 | 1 |
plus de 25 | 0 | 0 | 0 |
Totaux | 1 | 100 | 100 |
Avant d'effectuer le test du χ2, il convient de regrouper les classes qui contiennent des effectifs trop faibles, on regroupe donc les deux premières classes (moins de 10) et les trois dernières classes (plus de 16). C'est sur les résultats cumulés que l'on calcule le
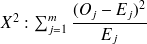, où m est le nombre de classes conservées, Oj est la valeur expérimentale observée dans cette classe et Ej la valeur théorique calculée pour cette classe. On obtient ainsi la valeur théorique d'un χ2 à m-k-1 degrés de liberté où k est le nombre de paramètres estimés à partir des données observées.
On a ici : m=3, k=1 (moyenne de 12 estimée) donc on doit obtenir un χ2 à un seul degré de liberté.
Le tableau ci-dessous résume le calcul du χ2:
Classes | Nombre de ca théoriques | Nombre de cas observés | X² |
moins de 10 | 34.8 | 31 | 0.415 |
11 à 15 | 49.7 | 48 | 0.058 |
plus de 16 | 15.5 | 21 | 1.952 |
Totaux | 100 | 100 | 2.425 |
L'extrait de la table du χ2 fournie en annexe permet de voir que, pour le degré de liberté 1, la probabilité est de 0,05 que la valeur du χ2 dépasse 3,84. Le test du χ2 est donc bien vérifié pour un seuil de 5%. Le test ne rejette donc pas l'hypothèse que les arrivées des clients suivent une loi de poisson de moyenne 12 pour une journée de 10h. Ce qui donne un taux d'arrivée
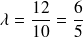
quel est le type de la file d'attente considérée ?
Nous avons donc une file du type M/M/1 (ou à défaut du type M/GI/1).
quel est le nombre moyen de voitures dans la station-service en comptant les voitures en attente et celle qui est sur le pont ?
Pour obtenir le nombre moyen de voitures dans la station en attente et en service, on peut appliquer la formule :
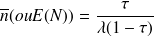avec
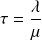, l'intensité de trafic,
soit pour l'application numérique
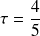et
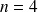
quelle est la durée moyenne de séjour d'une voiture dans la station ?
Pour obtenir la durée moyenne de séjour d'une voiture dans la station, on peut appliquer la formule:
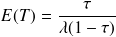soit pour l'application numérique
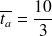d'heures
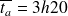
quel est le nombre moyen de voitures en attente ?
Pour obtenir le nombre moyen de voitures en attente, on peut appliquer la formule:
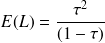soit pour l'application numérique
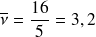
quelle est la durée moyenne de l'attente d'une voiture ?
Pour obtenir la durée moyenne de l'attente d'une voiture, on peut appliquer la formule:
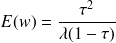soit pour l'application numérique
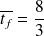d'heures
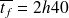
quel est le bénéfice journalier du garagiste ?
Pour obtenir le bénéfice moyen journalier du garagiste, il suffit d'utiliser le nombre moyen de voitures traité par jour et le bénéfice moyen constaté par voiture:
b = 12 x 50€ = 600 € b = 600 €
