L'existence d'un réseau de relations de voisinage entre pleins et vides
Ce réseau est la conséquence directe des propriétés d'homogénéité des parois.
Les règles fondamentales ci-dessus étant respectées, elles définissent sur les objets :
local
paroi (composant mur, plancher, plafond)
face filaire homogène
rive (de face)
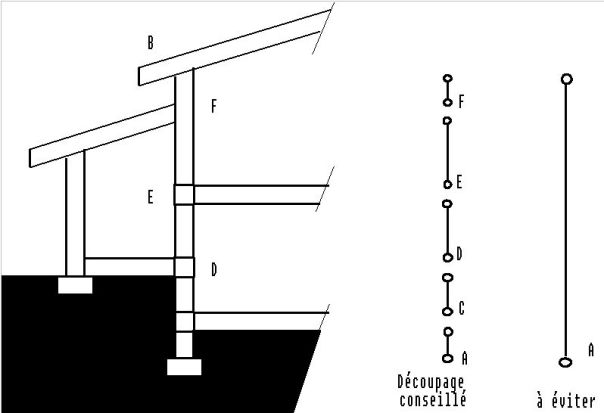
nœud (rive représentée par un point, sur un plan)
partition exclusive des entités de même nature,
attribut de ces entités,
un réseau relationnel qui permet par avance tout calcul de voisinage, de continuité, de dimensionnement, d'expression de règles de transformations locales, d'expression de règles de transformations contextuelles.
On comprend alors que l'opération qui consiste à transformer les parois décrites à travers la représentation AXES DE STRUCTURE soit en théorie toujours possible.
Définition :
Une paroi composant[1] de type plaque (comme un mur, un plancher) est dite homogène[2] quand elle sépare deux local[3], et seulement deux.
Dés lors, ses propriétés fonctionnelles et physiques sont supposées constantes sur toute sa surface.
Dès lors il existe une relation de voisinage[4] non ambiguë et réciproque entre le composant[1], le local[3], et tout autre objet situé dans leur environnement, comme le nu de local[5].
L'expérimentation a déjà montré qu'une chaîne de logiciels de métiers, utilisables seulement dans les activités de la conception, de la maintenance, et de la GTP[6], exploitait nécessairement les trois classes opposées de représentation du bâtiment.
A n'en pas douter, les logiciels techniques de la nouvelle génération, dans les prochaines années, seront tous obligés de manipuler ces concepts d'homogénéité, s'ils veulent assurer pleinement un rôle d'échange des données du projet, donc d'interopérabilité, à travers une maquette numérique.
En particulier, ils devront pouvoir extraire ou produire la représentation AXES DE STRUCTURE[7], si possible muni de la propriété d'homogénéité[8], pour se garantir une faisabilité d'échange dans le maximum de situations.
Fondamental :
Une représentation AXES DE STRUCTURE[7] dont les faces filaires sont homogènes[2] peut toujours être transformée automatiquement dans une des deux autres représentations graphiques : COMPOSANT[9], et NU DE LOCAUX[10].
Un utilisateur de logiciel technique ou de CAO[11], impliqué dans des échanges de données du projet, doit savoir reconnaître les performances de son outil et ses limites.
Il doit donc maîtriser les concepts de classification de ce chapitre.
Les concepts de LOCAL[3] et de NU DE LOCAL[5] ont été abordés dans le cours d'une manière intuitive. Ils correspondent aux définitions normalisées dans les IFC. C'est pourquoi ils sont notés en bleu soulignés.
Ces deux concepts IFC seront approfondis et illustrés.






