Correction
Option a : selon cette option, l'agence deviendrait un système M/M/1, avec
,
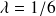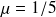ainsi que
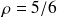.En utilisant la relation définie dans le cours sur le files M/M/2, on obtient alors :
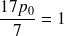et donc que
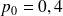
On peut donc en déduire que
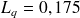et finalement que
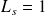client et
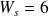minutes. Le dédoublement des employés entraîne donc une diminution spectaculaire du moyen passé par les clients dans l'agence, par un facteur de 5 environ.Option b: selon cette option, l'agence va se comporter comme une paire de systèmes M/M/1 indépendants. Analysons un de ces systèmes, disons celui des Géants (celui des Nains est identique). On peut supposer que le processus d'arrivée des Géants reste poissonien avec
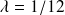et
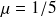. On a donc pour ce système,
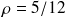et
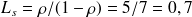client, ainsi que
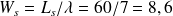minutes.Remarquons que
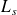est le nombre moyen de clients dans la section Géants donc en moyenne 1,4 client (Géants ou Nains) sont présents dans l'agence. Chacun de ces clients séjourne en moyenne 8,6 minutes dans l'agence. En terme de temps passé dans l'agence, l'option a est donc préférable à l'option b. Il s'agit là d'un principe généralement dans les systèmes à serveurs multiples : il est plus efficace de constituer une file d'attente unique et d'orienter chaque client vers le premier serveur disponible que de constituer des files distinctes pour chaque serveur.Option c: on retrouve ici un seul système M/M/1, comme dans la situation initiale, mais à présent
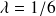et
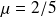, donc
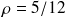. On a donc pour ce système :
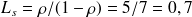client, ainsi que
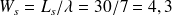minutes.
L'option C est donc la meilleure solution, bon courage a Gulliver pour l'expliquer au géant !
