Correction Question 3
Cas correspondant au serveur B semi-actif. (k=1)
Cas correspondant à la file d'attente à deux serveurs non identiques où les clients ne savent pas que B est plus rapide que A (ou le contraire). (k=1)
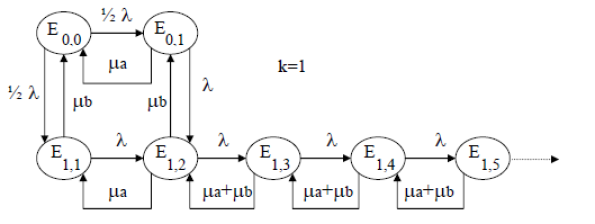
Cas correspondant à la file d'attente à deux serveurs non identiques où les clients savent que B est plus rapide que A. (k=1)
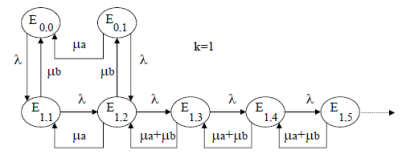
Comparaison : le deuxième cas (client n'ayant aucune connaissance des taux de service des deux guichets) est différent des deux autres. Le cas de la file d'attente à deux serveurs non identiques où les clients connaissent le guichet le plus rapide est analogue au cas du serveur inactif si le serveur toujours disponible (A) est le plus rapide des deux.
Application du théorème des coupes pour obtenir les équations du régime permanent
Pour n états, il faut n-1 coupes complétées par la somme des probabilités qui est égale à 1. Les coupes les plus naturelles (avec le moins possible d'arcs) sont celles qui sont représentées sur le graphe ci-dessus. (k=1)
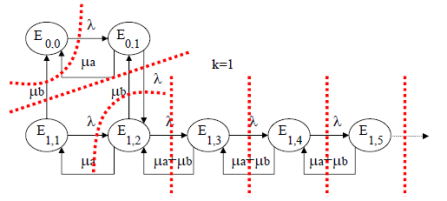
Les équations sont alors :
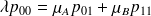
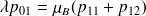
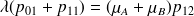
et toutes les équations « génériques »
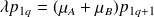
Grâce aux équations génériques, on peut calculer facilement tous les
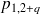en fonction de
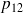pour
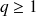
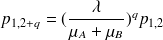
Grâce aux trois autres équations, on peut trouver
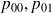et
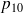en fonction de
.
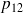Il aurait été également très intéressant de regarder la valeur des formules dans le cas particulier où μA = μB
En dehors de la distinction à faire pour
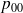et
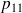, on retrouve bien M/M/2 ou M/M/2/S.
