Exercices de Files d'Attente

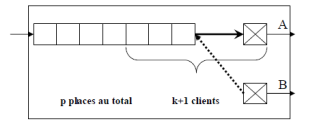
Un bureau de change, localisé à l'intérieur d'un centre commercial, comporte deux guichets pour servir les clients. Son local est très petit et ne peut pas contenir plus de p clients dans le système d'attente, y compris les clients que l'on est en train de servir : s'il y a déjà p clients dans le système d'attente, les clients qui arrivent poursuivent leur chemin, renonçant à faire du change ou cherchant une banque ou un autre bureau de change.

La clientèle du bureau de change ne justifie pas d'avoir en permanence ses deux guichets ouverts, néanmoins, pour des raisons de sécurité, il est important d'avoir en permanence deux personnes présentes dans le bureau de change, la deuxième personne pouvant effectuer d'autres tâches indépendantes des services directs aux clients lorsqu'elle n'est pas en train de servir les clients.

On a donc décidé la politique de fonctionnement suivante pour le bureau de change. Pendant les heures d'ouverture, le guichet A est toujours ouvert et son taux de service est μa (fonction de la plus ou moins longue expérience de la personne mise au guichet A). Le guichet B est en permanence affiché « fermé ». Néanmoins, la personne qui travaille derrière le guichet surveille la longueur de la file d'attente et s'il y a au moins k+1 clients dans le bureau (1 servi par A et k en attente), alors le guichet B se met à servir le premier client en attente dans la file. Son taux de service est μb. Lorsqu'il aura fini de servir le client, il se remettra à ses tâches habituelles si le nombre de clients dans le bureau est inférieur ou égal à k ou appellera le premier client en attente dans la file s'il y a au moins k+1 clients dans le bureau.

Fonctionnement de la File d'attente

On suppose que les demandes des clients peuvent être plus ou moins complexes et que l'on ne commet pas d'erreur en supposant que le système d'attente est sans mémoire, c'est-à-dire que les deux lois de service sont exponentielles et que les clients arrivent selon une loi de poisson dont on notera le paramètre λ. Le taux d'arrivée des clients est donc de λ (probabilité d'arrivée d'un client λdt sur l'intervalle de temps dt). On suppose également que dt est suffisamment petit pour que la probabilité de deux évènements simultanées soit négligeable (on ne représente pas les transitions en (dt)2).

Pour résumer, on a donc un système d'attente à deux serveurs non identiques (sauf si 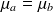), dont le serveur A n'est pas toujours actif (s'il n'y a pas de client ou si le guichet B est en train de finir un client dont le service était plus long que le dernier client traité par A), mais est toujours disponible alors que l'autre serveur B s'active de manière conditionnelle.

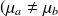et )

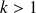Nous vous proposons ci-dessus le dessin du graphe associé à la chaîne de Markov décrivant le système d'attente du bureau de change. Chaque sommet du graphe correspond à un état dénoté par 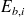, où b vaut 0 ou 1 et où i varie de 0 à k si b=0 et de 1 à p si b=1.

a) expliquer dans quel état est le système lorsqu'il est dans l'état .

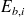b) compléter la chaîne de Markov en ajoutant les probabilités de transition sur les arcs du graphe.

Nous vous proposons ci-dessus le dessin du graphe associé à la chaîne de Markov décrivant le système d'attente du bureau de change ( 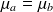et 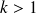). (k=3, p=7)

a) compléter la chaîne de Markov en ajoutant les probabilités de transition .

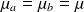b) on se place dans le cas très particulier où les deux serveurs ont des lois identiques et où k=1. Que pensez-vous de ce cas particulier ? A quel système d'attente peut-on considérer qu'il est équivalent et sous quelles conditions d'analyse des performances de ce système ?

( ).

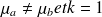Vous pouvez au choix prendre p=7 comme sur les graphes ci-dessus ou p=+∞.

1. dans le but de montrer que ce problème est différent

   • de celui d'une file d'attente à deux serveurs non identiques où les clients ne savent pas quel est le serveur le plus rapide (probabilité ½ de choisir l'un ou l'autre des serveurs lorsqu'ils sont tous les deux inoccupés, sinon le client va toujours sur le premier serveur qui se libère)

   • de celui d'une file d'attente à deux serveurs dont les clients savent que μb>μa (probabilité 1 de choisir le plus rapide B lorsque les deux serveurs sont inoccupés),

   dessiner (dans le cas k=1) les chaînes de Markov associées à ces trois cas (le problème considéré ici et les deux nouveaux problèmes de cette question) et comparer les.

2. en notant pb,i la probabilité d'être dans l'état Eb,i en régime permanent, utiliser le graphe dessiné dans le cas particulier de notre problème pour k=1 de la question précédente et le théorème des coupes afin d'obtenir le système d'équations qui permettraient d'obtenir tout d'abord toutes ces probabilités en fonction de p1,2 , puis la valeur de p1,2 en tenant compte du fait que la somme des probabilités de tous les états est toujours égale à 1.