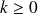Question 1
Paramètres :
Si
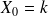 : S est l'instant d'arrivée du premier client, et T est l'instant de fin de service du premier client.
: S est l'instant d'arrivée du premier client, et T est l'instant de fin de service du premier client.
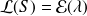
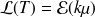 si
si
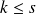 ou
ou
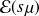 si
si
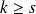
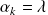
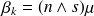 .
.
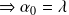
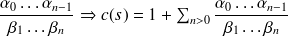
Or : Une loi de probabilité existe si et seulement si
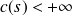
et alors on a :
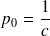 , et ,
, et ,
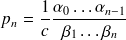
2 cas peuvent alors se présenter :
- Si
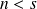 :
:
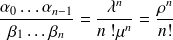
avec
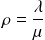
- Si
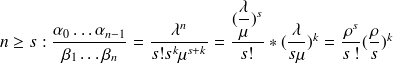
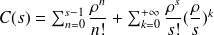
Donc
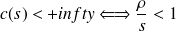 c'est à dire :
c'est à dire :
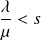
Or ceci est une condition nécessaire et suffusante pour justifier l'existence d'une probabilité limite.
Et alors
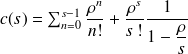
Interprétation des résultats :
Processus de poisson de paramètre
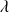
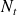 : Nombre d'entrée dans un intervalle de temps de longeur t.
: Nombre d'entrée dans un intervalle de temps de longeur t.
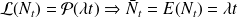
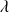 : Nombre moyen de clients entrant par unité de temps
: Nombre moyen de clients entrant par unité de temps
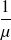 : Temps moyen de service d'un client
: Temps moyen de service d'un client
Le nombre moyen de clients entrant est indépendant du temps de service des clients.
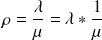 : quantité moyenne de service par unité de temps exigée (pour servir les clients).
: quantité moyenne de service par unité de temps exigée (pour servir les clients).
Pour qu'il y ait un régime permanent il faut (et il suffit) que la quantité moyenne de service exigée par unité de temps soit inférieur à s.
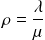 s'appelle le taux de trafic.
s'appelle le taux de trafic.
Et enfin, précisons tout de même que pour n<s:
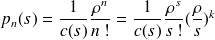
Avec :
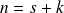 et
et