Exercices sur les chaînes de Markov en temps continu

On considère un système composé de s serveurs.

La règle est simple, le premier entré sera le premier servi.

Les clients entrent suivant un processus de poisson de paramètre 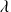(entrée poissonnienne illimité).

Le temps de service d'un client suit une loi

Soit 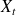: le nombre de clients présents dans le système

1. Donner les conditions pour l'établissement d'un régime permanent. (C'est à dire la loi de probabilité limite).

2. Dans le cas d'existence d'un régime permanent

   1. Calculer la loi limite

   2. Calculer 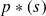 : probabilité qu'il y ait de l'attente

   3. Calculer 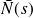 : longueur moyenne de la file d'attente

   4. Calculer 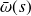  : temps moyen qu'un client passe à attendre d'être servi

3. Application dans un exemple : Un magasin de pièces détachées dans une grande entreprise .

Les ouvriers doivent s'y présenter pour obtenir des pièces . en moyenne, il y a 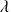ouvriers par heure qui s'y présentent. le temps moyen de service est de

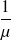
Le coût horaire d'un magasinier :

Le coût horaire d'un ouvrier inactif : (salaire + charge + manque à gagner)

Déterminer le nombre optimum de magasiniers (pour optimiser le coût de revient par heure du magasin)

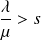et on pose : 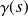: coût moyen horaire