loi de probabilité invariante
La chaîne de Markov étudiée est évidemment régulière puisqu'elle ne comporte qu'une seule classe. Nous savons donc qu'elle admet une unique loi de probabilité invariante p et elle est solution de
.
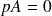
On procède donc au calcul. On note
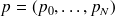un vecteur ligne. On a alors :
On remarque que les mêmes termes apparaissent d'une ligne à l'autre avec des signes opposés. On simplifie donc le système par sommes successives et on obtient :
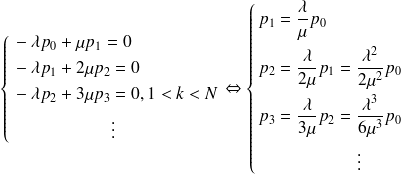
En fin de compte,
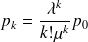. On pose
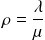. On traduit maintenant la deuxième propriété vérifiée pour déterminer
:
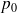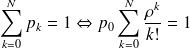
D'où finalement :
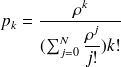
Remarque :
Si
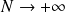alors
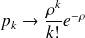une loi de Poisson de paramètre
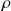. La loi que nous avons trouvée s'appelle la loi de Poisson tronquée à N (dans le sens où l'on ne dépasse pas la valeur N).
