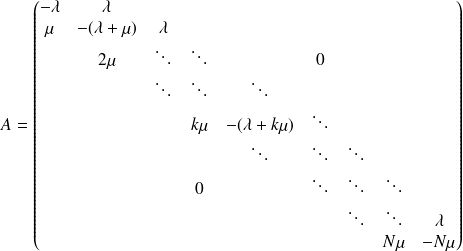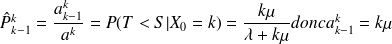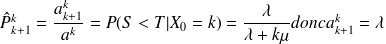Générateur infinitésimal
Le calcul du générateur infinitésimal se fait en deux parties :
calculer les termes diagonaux
calculer les autres termes
En effet, d'après les formules qui ont été vues dans le cours, les éléments du générateur infinitésimal sont calculables à l'aide des termes diagonaux qui peuvent se déduire d'après l'énoncé
Calcul des termes diagonaux
Pour calculer les termes du générateur infinitésimal, il faut se souvenir de leur interprétation probabiliste. Dans le cas des termes diagonaux, il s'agit de :
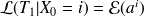où
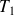est l'instant de la première transition.
Pour l'exercice, nous allons introduire deux variables :
S: l'instant d'arrivée de la première voiture
T: l'instant de départ de la première voiture en stationnement
On distinguera donc trois cas par la suite :
aucune voiture n'est stationnée :
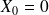
tout le parking est occupé :
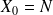
un nombre quelconque de voitures occupe le parking (autre que les deux cas précédent) :
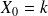
Parking vide
Si aucune voiture n'est stationnée, aucune voiture ne peut partir et donc le premier instant de transition est donné par S.
Or on sait de par l'énoncé que l'arrivée des voitures suit une loi
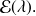D'après la formule que nous avons rappelée, on trouve donc :
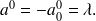
Parking saturé
Si le parking est saturé, aucune voiture ne peut arriver et donc l'instant de la première transition est donné par T.
Il faut donc déterminer la loi de T. Toutes les places sont occupées, cela signifie que l'instant de la première transition est donné par le départ de la première. Si on note
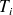l'instant de départ de la voiture stationnée à la place i. On sait alors que
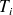suit une loi
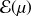. On peut alors dire que
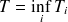. Les
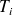sont indépendantes donc en se servant du rappel de l'énoncé on peut en conclure que T suit une loi
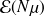. On en conclut donc finalement que :
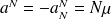
Nombre quelconque de voitures
Dans ce cas, on note k le nombre de voitures stationnées et U l'instant de la première transition.
L'instant de la première transition est alors donné par le temps le plus court entre le départ ou l'arrivée d'une voiture donc
. On sait que S suit une loi
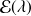et par un raisonnement tout à fait analogue à la partie précédente, on détermine que T suit une loi
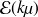. S et T étant indépendantes, on conclut que U suit une loi
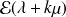. D'où on obtient :
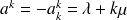
Calcul des autres termes
Pour calculer les autres termes du générateur infinitésimal, on se sert de la formule vue dans le cours :
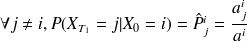. où
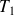est l'instant de la première transition. Évidemment on retrouvera les trois cas rencontrés lors du calcul des termes diagonaux, mais aussi on remarque que beaucoup de 0 vont apparaître. En effet, d'après le diagramme de transition,
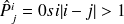puisque les transitions se font par saut de 1
Parking vide
Si aucune voiture n'est stationnée, on ne peut passer que de l'état 0 à l'état 1. On a donc que :
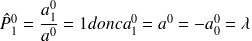
Parking saturé
Si le parking est saturé, on ne peut passer que de l'état N à N-1. On a donc que :
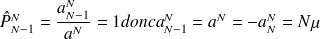
Nombre quelconque de voitures
On note k le nombre de voitures présentes dans le parking. On peut passer alors à l'état k+1 ou k-1. On obtient donc en reprenant les varaible S et T définies auparavant dans le calcul des termes diagonaux :
Générateur infinitésimal complet
Après ces calculs, on peut enfin écrire le générateur infinitésimal complet sous forme canonique :
