Temps moyen passé dans les états transitoires
Lorsque l'on modélise un processus par une chaîne de Markov en temps continu, on s'intéresse dans un premier lieu au temps que le processus est susceptible de passer dans un état donné. Par exemple, si on modélise une file d'attente, on peut s'intéresser au temps moyen pendant lequel elle sera vide. Les outils présentés dans cette partie permettent de calculer ce genre de résultats.
Définition :
On note
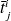le temps moyen passé dans l'état
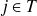r sachant qu'on est parti de
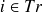. On note et on défini la matrice des temps moyens par :
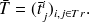
Méthode :
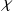est inversible et
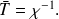
Remarque :
Il est possible de passer par la matrice de transition de la chaîne discrète associée.
On peut en effet l'utiliser pour calculer
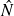la matrice du nombre moyen de passage par les états vue en temps discret avec la formule
.
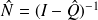Ensuite, nous avons vu que le temps passé entre deux transitions dans un état i suit une loi exponentielle
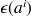. Cela signifie que le temps moyen passé dans cet état avant une transition est
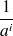(voir la moyenne d'une loi exponentielle).
Ainsi la connaissance du nombre moyen de fois que l'on passe par cet état avec le temps moyen qu'on y reste à chaque passage permet de connaître le temps total moyen que le système y est resté. On obtient finalement
