Théorème ergodique
Ce théorème est extrêmement puissant et c'est pourquoi nous avons voulu mettre l'accent dessus en lui dédiant une partie à son nom.
Méthode :
On suppose que E est fini et qu'il ne comporte qu'une seule classe finale. La classe finale constitue en elle même une chaîne régulière et porte donc une loi de probabilité invariante. Notons la
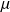. On l'étend à l'espace d'état tout entier en posant
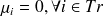. On a alors :
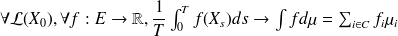
Ce que le théorème veut dire concrètement, c'est qu'un processus de Markov n'ayant qu'une classe finale se comporte pour des temps suffisamment longs comme s'il se résumait uniquement à cette classe finale.
En effet, nous savons déjà que le processus y entrera au bout d'un temps fini pour ne jamais en sortir après.
Il restera donc un temps fini dans la partie transitoire et un temps infini dans la partie finale. Il y a donc une certaine logique à ce que pour des temps élevés, le processus se résume à sa classe finale.
