Chaînes de Markov à temps continu régulière
Les chaînes de Markov à temps continue régulière sont des chaînes sur lesquelles on pourra définir des lois de probabilité invariantes. Ce sont donc des chaînes sur lesquelles on pourra étudier le comportement en régime permanent.
Rappel : Loi de probabilité invariante
Une loi de probabilité invariante sur une chaîne de Markov est un vecteur ligne
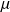tel que
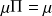donc que la loi est invariante quel que soit le nombre de transitions étudié.
Définition :
On dit que une chaîne est régulière si elle ne comporte qu'une classe (donc nécessairement finale).
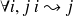(donc
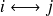) donc
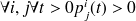(et réciproquement).
Méthode : Théorème fondamental sur les chaînes régulières
Supposons que nous ayons une chaîne régulière.
Il existe alors une et une seule loi de probabilité invariante définie dessus. Notons la
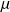. Celle-ci vérifie :
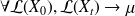exponentiellemnt vite-
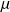est l'unique solution de
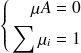
Ce théorème permet de caractériser complétement la loi de probabilité invariante d'une chaîne régulière et permet de ce fait d'étudier le comportement d'un système en régime permanent. Par exemple, c'est grâce à cette loi de probabilité invariante que l'on peut étudier le modèle de file d'attente d'Erlang.
