La recherche du niveau de production qui maximise le résultat a conduit à la conclusion suivante : cette production est celle pour laquelle "le coût marginal est égal à la recette marginale"
Nous voudrions confirmer cette conclusion par l'observation du graphique sur lequel nous portons les quatre courbes représentatives :
- du coût moyen et du coût marginal,
- de la recette moyenne et de la recette marginale.
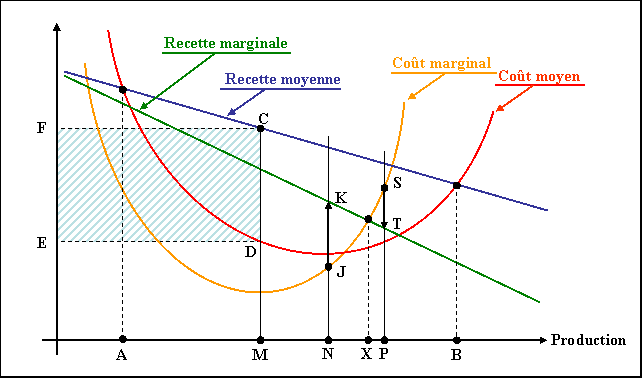
Sur ce graphique, on reconnaît d'abord les "seuils de rentabilité", chiffres d'affaires pour lesquels les charges totales correspondent strictement à la recette totale, soit donc aussi : coût moyen = recette moyenne ; ils correspondent aux points A et B ; la production doit donc se situer entre ces bornes.
D'autre part, si la production se situe au niveau figuré par le point M, le résultat unitaire moyen est figuré par le segment de droite : CD, et donc le bénéfice total est figuré par le rectangle CDEF.
On se demande s'il serait intéressant d'accroître la production d'une unité, la portant du niveau M au niveau N.
Réponse affirmative, car cette unité supplémentaire dégage, pour elle seule, un "résultat marginal" positif, figuré par le segment de droite JK.
Par contre, si la production d'une unité supplémentaire avait fait passer la production totale du niveau M au niveau P, la réponse eût été négative, car le "résultat marginal" de l'unité supplémentaire eût été négatif ; il est figuré par le segment ST : cette unité coûte plus qu'elle ne rapporte.
On voit donc qu'il est intéressant de "pousser" la production jusqu'au niveau X mais non au-delà puisque, à partir de ce niveau, le coût marginal devient supérieur à la recette marginale.

