Un exemple de modèle conceptuel d'objets du bâtiment
Pour faciliter la démarche pédagogique, nous illustrerons par quelques schémas une petite partie d'un modèle qui décrit une des familles d'objets du bâtiment : les composants.
Dans la terminologie IFC, les composants sont des produits[1].
Il est important de situer ce concept par rapport aux autres concepts de même niveau manipulés dans les IFC.
Les schémas montrés dans cet ouvrage adoptent eux mêmes des conventions graphiques structurées, normalisées. En attendant d'apprendre ce formalisme, souvent utilisé pour exprimer les schémas conceptuels, nous les expliquons (pour information on utilise le formalisme NIAM[2], qui est développé dans l'unité de cours suivante).
Un modèle conceptuel comprend trois sortes de concepts, déjà examinés par ailleurs :
l'objet[3], compris dans le sens de classe[4], que l'on appelle parfois aussi tout simplement un concept[5] . Exemple : mur est un concept. Pour ne pas provoquer d'ambiguïté de vocabulaire, il faudrait toujours dire « classe d'objets », le terme « objet » étant réservé à un individu de la classe (une occurrence).
les relations[6], qui relient les objets. Un schéma qui décrit un modèle doit être simple. C'est pourquoi en général on préfère n'utiliser des relations que limitées à deux objets. On appelle ces relations « binaires ».
Exemple : la relation de calage « repose sur » lie les objets « plancher » et « mur ». On s'aperçoit qu‘une relation à un sens direct : « repose sur », et un inverse : « est supporté par ».
les attributs[7] , ou propriétés[8] qui portent sur les objets, et aussi sur les relations.
Exemple : un type de mur est caractérisé par une série de types de propriétés (épaisseur, dimensions, matériaux, couleur ...). De plus, une occurrence de mur, c'est à dire un morceau de mur réel, inséré dans un projet, devient un individu de la classe mur, auquel on peut associer un numéro d'identification (unique), et pour lequel les propriétés prennent une valeur.
Une partie d'un modèle qui regroupe deux objets, une relation et des propriétés s'appelle une « idée[9] ». Une idée est une description élémentaire de telle sorte que pour l'usage que l'on doit en faire ne subsiste aucune ambiguïté. Chaque personne qui essaie de comprendre une idée doit en tirer la même signification.
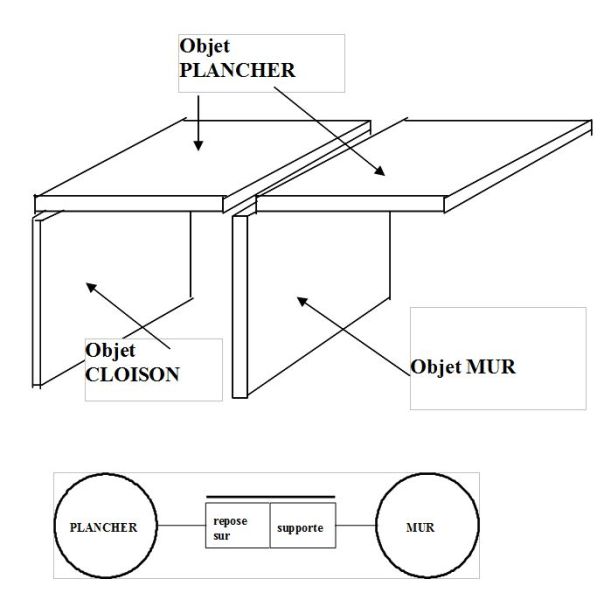
Le schéma ci-dessus exprime l'idée à approfondir ou à laisser en l'état, pour indiquer à un logiciel de calcul de descente de charge comment s'y prendre. Traduction :
un plancher ne peut reposer sur aucun mur (parce que la solution poutre existe) ou reposer sur un seul mur (parce que le plancher peut être en porte à faux) ou sur plusieurs murs, tandis qu'en lecture inverse, un mur peut supporter un ou plusieurs planchers ou aucun.






