Historique
La Programmation Linéaire est un cadre mathématique général permettant de modéliser et de résoudre certains problèmes d'optimisation. Mathématiquement le problème consiste à Optimiser une Fonction Linéaire sous des Contraintes Linéaires liant les variables
Historiquement, la programmation linéaire a été développée et utilisée en 1947 par George Bernard Danzig, Marshall Wood et leurs collaborateurs au U.S. Department of the Air Force. Les premières applications se situaient dans le domaine militaire mais elles se sont rapidement déplacées vers l'industrie et la planification économique : il s'agit par exemple de déterminer la production maximisant le bénéfice compte tenu de ressources limitées ou minimisant les coûts tout en garantissant une production donnée, de résoudre des problèmes d'allocation de ressources limitées en vue d'atteindre des objectifs fixés, ...
Exemple : Exemple illustratif
Donnons tout d'abord un exemple concret : un Problème de Production
Une entreprise fabrique deux produits P1 et P2, chacun nécessitant l'utilisation de 3 machines M1, M2 et M3 disponibles respectivement 9900 mn, 8400 mn et 9600 mn par semaine. Une unité de produit P1 utilise 11 mn de M1, 7 mn de M2 et 6 mn de M3. De même une unité de produit P2 a besoin de 9 mn de M1, 12 mn de M2 et 16 mn de M3. Les bénéfices de vente par unité de produit sont respectivement de 900 € pour P1 et de 1 000 € pour P2.
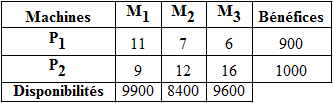
Une solution de ce problème consiste à fixer le volume de production de ces deux produits. Notons x1 (resp. x2) le nombre d'unités de P1 (resp. P2) produites ; x1 et x2 sont les variables de décision de notre problème. Le but est de déterminer la production optimale hebdomadaire, c'est-à-dire le nombres d'unités de fabrication de P1 et P2 donnant le bénéfice maximum par semaine compte tenus des disponibilités des machines.
Il faut donc de chercher le maximum de la fonction économique (ou objectif)
égale au bénéfice hebdomadaire correspondant à la fabrication d'une quantité x1 de produit P1 et d'une quantité x2 de produit P2 avec les contraintes suivantes :
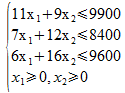
Elles correspondent à la fois aux durées de fabrication de chacun des produits, aux disponibilités des trois machines et enfin au fait que les quantités produites sont positives. C'est donc bien un problème classique de Programmation Linéaire : il s'agit en effet de déterminer le maximum d'une fonction linéaire sous des contraintes linéaires.
