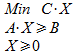Plus généralement supposons que l'on fabrique n produits en utilisant m machines tels que le produit j rapporte un bénéfice de cj et nécessite un temps aij sur la machine i qui n'est disponible qu'un temps bi alors le calcul de la production optimale, c'est à dire celle donnant le bénéfice maximal, revient à déterminer les quantités xj de produit j qui maximisent la fonction économique
sous les contraintes :
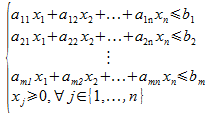
C'est ce que l'on appelle la Forme Canonique d'un problème de Programmation Linéaire. On notera PLFC ce problème.
Si l'on note C le vecteur ligne des cj, B le vecteur colonne des bi (bi ≥ 0) , X le vecteur colonne des variables xj et A la matrice m.n des aij, le problème est alors de calculer
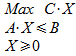
Remarque :
Dans la présentation précédente la problématique consiste à Maximiser une Production en tenant compte de ressources limitées, de façon symétrique, ou « duale », de nombreux problèmes consistent à Minimiser des Coûts de production tout en assurant des objectifs économiques, si les fonctions intervenant sont linéaires ces problèmes peuvent alors se formuler de la façon suivante :