Nous allons maintenant montrer comment interpréter et exploiter les coefficients du tableau simplexe final lorsque l'on modifie certaines données du problème. C'est ce que l'on appelle aussi l'analyse de sensibilité ou l'analyse post optimale.
Pour cela, nous allons reprendre le problème de production :
Rappel :
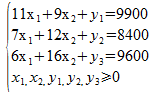

Dans cet exemple, nous allons nous intéresser à deux questions :
• Que se passe t'il si l'on dispose de 60 min de plus sur M1 ?
• De combien de temps sur M2 faudrait-il en plus pour utiliser tout le temps de disponibilité de M3 ? Quelles sont alors la nouvelle production et le nouveau profit ? À quelle condition sur le coût d'utilisation de M2 cette opération est-elle rentable ?
Augmentation du temps d'utilisation de M1
On peut bien sûr résoudre à nouveau le problème en remplaçant le terme constant dans la première équation par 9 960. L'exploitation des équations finales permet cependant l'interprétation suivante : toute variation δ1 de y1 donc du temps de machine disponible sur M1 se traduit par :
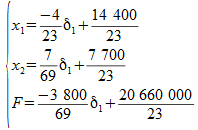
Donc si l'on dispose de 60 mn supplémentaires sur M1, ce qui correspond à δ1 = - 60, car y1 représente le temps de disponibilité restant, nous obtenons donc la nouvelle production :
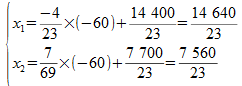
et le nouveau bénéfice :
Géométriquement cela revient à déplacer le côté A3A4 sur la droite, autrement dit on pourrait retrouver les résultats obtenus en résolvant le système d'équations :
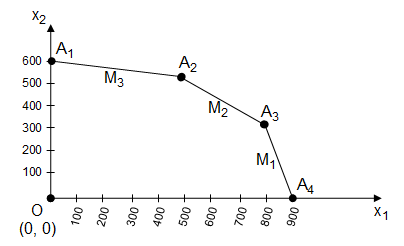
Remarque :
Compte-tenu des temps disponibles sur M2 et M3, il n'est pas possible d'augmenter indéfiniment le bénéfice en augmentant la disponibilité de M1. Dans ce cas, la contrainte M2 sera la première bloquante lorsque :
Ce qui correspondrait à une disponibilité de M1 égale à 13 200 min. S'agissant d'une production hebdomadaire, il paraît cependant difficile d'augmenter le temps de disponibilité de M1 à plus de 9 jours...
Utilisation complète de M3
À l'optimum, la troisième équation montre que le temps supplémentaire δ2 d'utilisation de M2 nécessaire pour utiliser tout le temps de disponibilité de M3 (y3 = 0), le temps d'utilisation de M1 restant le même (y1 = 0), doit vérifier :
Nous obtenons donc :
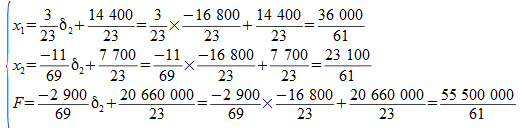
Géométriquement cela revient à déplacer le côté A2A3 vers l'extérieur du polygone jusqu'à l'intersection des droites A1A2 et A3A4, autrement dit on pourrait retrouver les résultats obtenus en résolvant le système d'équations :
Remarque :
La fonction économique augmente proportionnellement à l'augmentation du temps de machine, le rapport est de 2 900/69, donc si le prix à la min est inférieur à cette valeur l'opération est rentable, sinon elle ne l'est pas.
