Nous allons maintenant nous intéresser à la résolution des programmes linéaires. Dans un premier temps nous allons étudier une méthode de résolution graphique. Revenons à notre premier exemple.
Rappel : Programme linéaire du problème de production
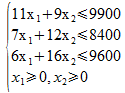
Comme il n'y a que deux variables x1 et x2, on peut les interpréter comme les coordonnées d'un point dans le plan, et les 5 contraintes linéaires définissent alors des demi-plans. Les points solutions correspondent donc à l'intersection de ces demi-plans, on obtient alors :
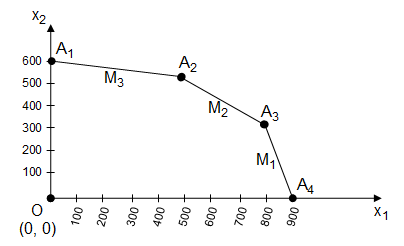
L'ensemble des solutions admissibles, ou réalisables, c'est-à-dire des couples (x1, x2), donc des points, vérifiant toutes les contraintes est exactement l'ensemble des points intérieurs au polygone convexe (O, A1, A2, A3, A4) frontières comprises, car les inégalités sont au sens large. Les côtés A1A2, A2A3 et A3A4 correspondent respectivement aux contraintes imposées par les limitations des temps d'utilisation des machines M3, M2 et M1.
Comme F = 900 x1 + 1 000 x2 on a x2 = - 9/10 x1 + F/1 000, le problème consiste donc à chercher, parmi l'infinité de droites « d'iso bénéfice » (ou d'équiprofit) ayant toutes les mêmes pentes, à savoir – 9/10, celle donnant le bénéfice maximum, elle correspond à la droite ayant la plus grande ordonnée à l'origine :
Ici il s'agit de la droite passant par le point A3 (14 400 / 23, 7 700 / 23), le bénéfice correspondant est alors de 20 660 000 / 23.
Remarque :
Remarquons que pour des raisons de convexité la valeur optimale est nécessairement obtenu en un point extrême du polygone, donc en O ou A1 ou A2 ou A3 ou A4. Il suffit donc de repérer ces points, d'y calculer F et d'en retenir la valeur maximale. La recherche d'une solution optimale parmi le nombre infini de solutions possibles se ramène donc au calcul de F sur un nombre fini de points, les sommets du polygone des contraintes
