Un consommateur peut acheter 4 types d'aliments dont les teneurs en calories et en vitamines ainsi que les prix à l'unité sont données par le tableau ci-dessous :
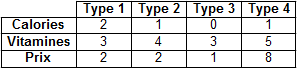
On cherche à obtenir, au moindre coût, une teneur minimale en vitamines de 7 et au moins 12 calories.
Ce problème est appelé le Problème du Consommateur, il s'agit de minimiser le coût d'un achat tout en garantissant des avantages minimaux.
Si l'on désigne par xi la quantité de produit i à acheter, alors la fonction à minimiser est :
sous les contraintes :
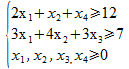
Complément : Variante de ce problème
Une variante de ce problème consiste à s'intéresser à un vendeur concurrent voulant s'approprier le marché avec deux types d'aliments dont les teneurs en calories et en vitamines par unité de volume sont respectivement de 1 et 0 pour le premier et 0 et 1 pour l'autre, et dont l'objectif sera donc d'offrir la plus grande quantité possible de calories et de vitamines à un prix inférieur ou égal : il recherche donc les quantités y1 et y2 de ses deux produits qui maximisent la fonction :
sous les contraintes :
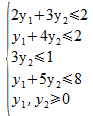
En utilisant une notation matricielle, le problème du consommateur correspond à :
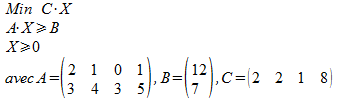
et celui du vendeur concurrent :
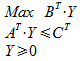
C'est un exemple de ce que l'on appelle la DUALITE en Programmation Linéaire, ces deux problèmes sont « duaux » l'un de l'autre et l'on peut montrer qu'ils ont le même optimum.
