Partie 1
Etude de la loi d'arrivées
Une station de lavage est ouverte chaque jour ouvrable, de 10h à 18h, sans interruption.
Une étude statistique a tout d'abord consisté à observer le nombre de clients qui arrivent pendant 130 périodes de 30 minutes. On s'est assuré, au préalable, de la stationnarité du processus.
Le nombre de clients arrivant durant chaque intervalle est décompté. On regroupe les résultats de l'enquête dans le tableau suivant :
Nombre d'arrivées en 30 min | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
Nombre d'observations | 5 | 12 | 22 | 23 | 18 | 13 | 6 | 4 | 1 | 1 | 0 |
Questions
Calculer l'espérance de cette distribution (par intervalle de 30 min).
On va supposer que la loi des arrivées est une loi de Poisson dont la densité s'exprime par :
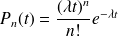
Quel serait alors le paramètre de cette loi ? Par le biais d'un test du
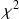, vérifier que ce modèle convient, au niveau 5%.Indication : On pourrait s'aider du tableau suivant :
Tableau récapitulatif du test N
Fréquences observées
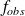
Fréquences théoriques
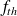
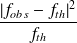
0
1
2
3
4
5
6
7
>7
Conclure sur le modèle choisi.
