Correction Question 1
Il s'agit ici de deux files d'attente entrelacées, on ne peut ni classer ce problème selon les notations de Kendall ni utiliser les formules pré-calculées fournies dans le polycopié. Il faut donc établir les formules de ce phénomène particulier d'attente.
Les états du système sont les
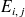 où i désigne un nombre de taxis en attente et j un nombre de clients en attente. On a selon l'énoncé: 0≤i≤3 et 0≤j≤3, mais aussi i.j=0 puisqu'il ne peut y avoir des taxis en attente que s'il n'y a pas de clients en attente et vice versa.
où i désigne un nombre de taxis en attente et j un nombre de clients en attente. On a selon l'énoncé: 0≤i≤3 et 0≤j≤3, mais aussi i.j=0 puisqu'il ne peut y avoir des taxis en attente que s'il n'y a pas de clients en attente et vice versa.
Les seules états possibles sont donc:
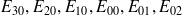 et
et
 . Pour les trois premiers il y a 3, 2 et 1 taxis en attente et pour les trois derniers il y a 1, 2 et 3 clients en attente. On note
. Pour les trois premiers il y a 3, 2 et 1 taxis en attente et pour les trois derniers il y a 1, 2 et 3 clients en attente. On note
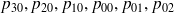 et
et
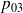 les probabilités du régime permanent de ces 6 états.
les probabilités du régime permanent de ces 6 états.
Pour établir le système d'équations permettant de trouver le régime permanent, le mieux est une fois de plus de dessiner le graphe de la chaîne de Markov associée (en ne représentant ni les boucles ni les
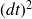 et en simplifiant par
et en simplifiant par
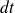 ) et d'utiliser les théorèmes des coupes. Néanmoins, pour ceux qui le souhaitent, voici la matrice de transition obtenue en négligeant les termes en
) et d'utiliser les théorèmes des coupes. Néanmoins, pour ceux qui le souhaitent, voici la matrice de transition obtenue en négligeant les termes en
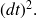
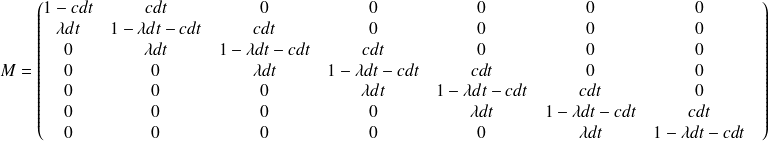
On peut obtenir les formules recherchées en développant la formule
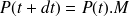 puis en mettant chaque ligne sous la forme :
puis en mettant chaque ligne sous la forme :
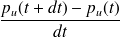
en faisant tendre dt vers 0, d'où en régime permanent la dérivée du premier membre devient nul et on obtient le résultat.
Mais une fois de plus il est plus simple d'utiliser le théorème des coupes (ou même directement le fait que l'on a reconnu un processus de naissance et de mort), en utilisant le graphe des transitions (sans les boucles) :
En commençant prenant les coupes à partir de la droite et en posant
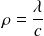 , on obtient successivement:
, on obtient successivement:
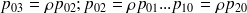 et
et
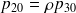
d'où:
 ... et
... et

Comme la somme des probabilités doit faire 1, on obtient immédiatement que:
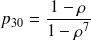 ,
,
comme avec les valeurs numériques de l'énoncé, on a
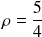 , on obtient:
, on obtient:
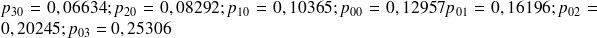
(dont la somme est égale à 0,99995)





