Exercices des Files d'Attente partie 2

A une station de taxis, prévue pour un maximum de trois taxis, les véhicules arrivent suivant une loi de Poisson de taux 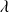( 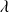exprimant une cadence par minute, prise égale à 1 pour l'application numérique). S'il n'y a pas de place, les nouveaux taxis qui arrivent passent sans s'arrêter.

On suppose les arrivées des clients également poissonniennes, au taux c par minute (avec c>1, c prendra la valeur 5/4 pour l'application numérique). Lorsque trois clients attendent, le suivant se dirige vers une autre station de taxis voisine.

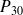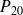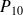1. Calculer les probabilités , et pour qu'il y ait 3, 2 ou 1 taxis en attente, 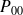pour qu'il n'y ait ni taxi, ni client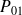, 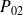et , et 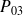pour qu'il y ait 1, 2 ou 3 clients en attente.

2. Combien de taxis par heure arrivent à hauteur de la station sans pouvoir s'arrêter ?

3. Combien de clients, par heure, ne s'arrête pas à la station par suite de l'affluence ?

4. Quels sont les temps moyens d'attente pour les taxis et pour les clients ?